空間における直線の方程式,平面の方程式

== 空間における直線と平面 == ≪目次≫ …項目名をクリックすれば，目的地に行けます

1.　直線と平面の交点の座標
2.　2平面の交線の方程式
3.　直線と点を含む平面の方程式
4.　直線1を含み直線2と平行な平面の方程式

（交わる2直線を含む平面の方程式）

（2点を通り平面に垂直な平面の方程式）

別のページにある目次

1. 1点を通り方向ベクトル $\vec{u}$ に平行な直線の方程式
2. 1点を通り直線2に平行な直線1の方程式
3. 2点を通る直線の方程式
4. 点と直線の距離
5. 平行な2直線間の距離
6. ねじれの位置にある2直線間の距離
7. 直線の方向余弦
8. ２直線のなす角

1. 法線ベクトルによる平面の方程式
2. 2つのベクトルで張られる平面の方程式
3. 3点を通る平面の方程式
4. 点と平面の距離
5. ヘッセの標準形
6. 2平面のなす角
7. 2平面の交角を二等分する平面

1.　直線と平面の交点の座標

【例題1】
　次の直線と平面の交点の座標を求めてください．

直線 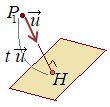$\frac{1-x}{3}=y-1=\frac{z+ 4}{2}$ ，平面 $x-2y+ 3z+ 10=0$

（解答）
$\frac{1-x}{3}=y-1=\frac{z+ 4}{2}$ とおく．

$x=1-3t$
$y=t+ 1$
$z=2t-4$
が平面の方程式を満たすようなｔの値を求める
$(1-3t)-2(t+ 1)+ 3(2t-4)+ 10=0$
$1-3t-2t-2+ 6t-12+ 10=0$
$t-3=0$
$t=3$
このとき， $(x,\hspace{2}y,\hspace{2}z)=(-8,\hspace{2}4,\hspace{2}2)$ …（答）

（生成AIを使って，解き方を指定しなければ，ChatGPT, Google Gemini, Microsoft Copilotのいずれでも，上記のｔを求める答案が示される）

（別解）…行列を用いた解き方
与えられた直線は､２つの平面 $\frac{1-x}{3}=y-1$ ， $y-1=\frac{z+ 4}{2}$ の交線だから，求める点は，３つの平面

$\frac{1-x}{3}=y-1$
$y-1=\frac{z+ 4}{2}$
$x-2y+ 3z+ 10=0$
の交点になる．すなわち

$x+ 3y+ 0z=4$
$0x+ 2y-z=6$
$x-2y+ 3z=-10$
この連立方程式をクラメルの公式や逆行列を使う方法で解けばよい．

≪クラメルの公式≫
$x=\frac{\begin{vmatrix}4& 3& 0\\6& 2& -1\\-10&-2& 3\end{vmatrix}}{\begin{vmatrix}1& 3& 0\\0& 2& -1\\1&-2& 3\end{vmatrix}}=-8$

$y=\frac{\begin{vmatrix}1& 4& 0\\0& 6& -1\\1&-10& 3\end{vmatrix}}{\begin{vmatrix}1& 3& 0\\0& 2& -1\\1&-2& 3\end{vmatrix}}=4$

$z=\frac{\begin{vmatrix}1& 3& 4\\0& 2& 6\\1&-2& -10\end{vmatrix}}{\begin{vmatrix}1& 3& 0\\0& 2& -1\\1&-2& 3\end{vmatrix}}=2$

≪逆行列を用して解く方法≫
$\begin{pmatrix}1& 3& 0\\0& 2& -1\\1&-2& 3\end{pmatrix}^{-1}$
$=\begin{pmatrix}4& -9& -3\\-1& 3& 1\\-2& 5& 2\end{pmatrix}$
$\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}4& -9& -3\\-1& 3& 1\\-2& 5& 2\end{pmatrix}\begin{pmatrix}4\\6\\-10\end{pmatrix}$
$=\begin{pmatrix}-8\\ 4\\2\end{pmatrix}$

【問題1.1】　
　次の直線と平面の交点の座標を求めてください．

直線 $\frac{x-3}{2}=\frac{y+ 4}{3}=\frac{z-5}{4}$ ，
平面 $2x-y+ 2z-2=0$

解答を見る解答を隠す

（解答）
$(x,\hspace{2}y,\hspace{2}z)=(3,\hspace{2}-4,\hspace{2}5)+ t(2,\hspace{2}3,\hspace{2}4)$

$x=2t+ 3$
$y=3t-4$
$z=4t+ 5$
が平面の方程式を満たすようなｔの値を求める
$2(2t+ 3)-(3t-4)+ 2(4t+ 5)-2=0$
$4t+ 6-3t+ 4+ 8t+ 10-2=0$
$9t+ 18=0$
$t=-2$
このとき， $(x,\hspace{2}y,\hspace{2}z)=(-1,\hspace{2}-10,\hspace{2}-3)$ …（答）

ChatGPT, Google Gemini, Microsoft Copilotのいずれも，「3次元空間における直線(x-3)/2=(y+4)/3=(z-5)/4と平面2x-y+2z-2=0の交点の座標を求めよ．」という形で質問を書き込むと，上記と同答案が示される．

--問題と解答--

【問題1.2】　
　次の直線と平面の交点の座標を求めてください．

直線 $x-2=\frac{y}{-2}=\frac{z-1}{3}$ ，平面 $x+ y+ 2z+ 1=0$

解答を見る解答を隠す

$(x,\hspace{2}y,\hspace{2}z)=(1,\hspace{2}2,\hspace{2}-2)$ …（答）

【問題1.3】　
　次の直線と平面の交点の座標を求めてください．

直線 $\frac{x+ 1}{-2}=\frac{y-2}{3},\hspace{2}z=1$ ，平面 $3x-2y+ 4z-9=0$

解答を見る解答を隠す

$(x,\hspace{2}y,\hspace{2}z)=(1,\hspace{2}-1,\hspace{2}1)$ …（答）

2.　2平面の交線の方程式

【例題2】
　次の2平面の交線の方程式を求めてください．

$x-y-z-3=0$ ， $2x+ y-z-4=0$

（解答）…高校数学の解き方
連立方程式と考えると

$x-y-z-3=0$
$2x+ y-z-4=0$
は，未知数が3個，方程式が2個だから不定解になる．そこで，どれか１文字，例えばzについては解かないことに決めて，x, yをzで表す．かっこ(　)内の文字については解かない．

$x-y=(z+ 3)$ …(1)
$2x+ y=(z+ 4)$ …(2)
(1)+(2)
$3x=(2z+ 7)$
(1)×2−(2)
$-3y=(z+ 2)$
$z=t$ を任意定数として，この結果を表すと

$3x=2t+ 7$
$-3y=t+ 2$
$z=t$
媒介変数と消去して直線の方程式を標準形にすると
$\frac{3x-7}{2}=-3y-2=z$ …（答）

ChatGPT, Google Geminiのいずれも，「次の2平面の交線の方程式を求めてください． x-y-z-3=0 ,2x+ y-z-4=0 」という形で質問を書き込むと，上記と同様の答案が示される（パラメータの選び方により，見かけの形は異なる形式になる）．Microsoft Copilotで解くと，答えが合わない??

【問題2.1】　
　次の2平面の交線の方程式を求めてください．
$2x+ y-3z+ 3=0,\hspace{5}3x+ y-2z=0$

解答を見る解答を隠す

（解答）
高校数学で（行列を使わずに）解く
未知数が３個で方程式が2個だから不定解になる．zについては解かないことに決める．
かっこ(　)内の文字については解かない．

$2x+ y=(3z+ 3)$ …(1)
$3x+ y=(2z)$ …(2)
第2式から第1式を引く
$x=(-z+ 3)$
この結果を第1式に代入する
$y=(5z-9)$
$z=t$ とおいて媒介変数 $t$ で表すと

$x=-t+ 3$
$y=5t-9$
$z=t$
媒介変数を消去して標準形で書くと
$\frac{x-3}{-1}=\frac{y+ 9}{5}=z$ …（答）

【問題2.2】　
　次の2平面の交線の方程式を求めてください．
$x-2y+ 2z=5,\hspace{5}x+ y-4z=2$

解答を見る解答を隠す

$\frac{x-3}{2}=\frac{y+ 1}{2}=z$ …（答）

【問題2.3】　
　次の2平面の交線の方程式を求めてください．
$2x-y+ z-3=0,\hspace{5}-3x+ 5y-2z+ 1=0$

解答を見る解答を隠す

$\frac{x-2}{-3}=y-1=\frac{z}{7}$ …（答）

3.　直線と点を含む平面の方程式

【例題3】

　直線 $x-1=\frac{y+ 2}{2}=\frac{z-3}{3}$ と点 $P(2,\hspace{2}3,\hspace{2}1)$ を含む平面の方程式を求めてください．

（解答）…3点を通る平面として求める

直線 $x-1=\frac{y+ 2}{2}=\frac{z-3}{3}$ の方程式を，媒介変数表示で表わすと

$x=t+ 1$
$y=2t-2$
$z=3t+ 3$
だから，例えばt=0, 1とすると直線上の２点 $Q(1,\hspace{2}-2,\hspace{2}3)$ , $R(2,\hspace{2}0,\hspace{2}6)$ の座標が得られる．
　そこで，これら3点P,Q,Rを通る平面の方程式を $ax+ by+ cz+ d=0$ とおいて， $a,\hspace{2}b,\hspace{2}c,\hspace{2}d$ を求めるとよい．（比率のみ定まる）
$P(2,\hspace{2}3,\hspace{2}1)$ を通るから
$2a+ 3b+ c+ d=0$ …(1)
$Q(1,\hspace{2}-2,\hspace{2}3)$ を通るから
$a-2b+ 3c+ d=0$ …(2)
$R(2,\hspace{2}0,\hspace{2}6)$ を通るから
$2a+ 6c+ d=0$ …(3)
未知数が4個，方程式が3個だから不定解になる．そこで $d$ については解かないことにして，他の文字を $d$ で表す．

$2a+ 3b+ c=(-d)$ …(1’)
$a-2b+ 3c=(-d)$ …(2’)
$2a+ 6c=(-d)$ …(3’)
(1’)−(2’)×2
$7b-5c=(d)$
(3’)−(2’)×2
$4b=(d)$
$b=\frac{d}{4},\hspace{3}c=\frac{3}{20}d,\hspace{3}a=-\frac{19}{20}d$
$a:b:c:d=-\frac{19}{20}:\frac{1}{4}:\frac{3}{20}:1=-19:5:3:20$
ゆえに
$-19x+ 5y+ 3z+ 20=0$ …（答）

（別解1）…平面を張る2つのベクトルで表示する方法

点 $P_1(x_1,\hspace{2}y_1,\hspace{2}z_1)$ を通り２つの1次独立なベクトル $\vec{l_1}=(l_1,\hspace{2}m_1,\hspace{2}n_1)$ ， $\vec{l_2}=(l_l,\hspace{2}m_2,\hspace{2}n_2)$ で張られる平面のベクトル表示は
$\vec{x}=\vec{OP_1}+ s\vec{l_1}+ t\vec{l_2}$
いま１つのべクトルとして， $\vec{l_1}=(1,\hspace{2}2,\hspace{2}3)$ が使える．もう１つのベクトルとして， $\vec{l_2}=\vec{PQ}=(-1,\hspace{2}-5,\hspace{2}2)$ を使う．
$(x,\hspace{2}y,\hspace{2}z)=(2,\hspace{2}3,\hspace{2}1)+ s(1,\hspace{2}2,\hspace{2}3)+ t(-1,\hspace{2}-5,\hspace{2}2)$
成分に分けて媒介変数表示にすると

$x=2+ s-t$ …(1)
$y=3+ 2s-5t$ …(2)
$z=1+ 3s+ 2t$ …(3)
この媒介変数表示から，２つの媒介変数を消去して，x,y,zの方程式にすればよい
(1)から $s=x-2+ t$
これを(2)(3)に代入

$y=3+ 2(x-2+ t)-5t$
$z=1+ 3(x-2+ t)+ 2t$

$-2x+ y+ 1+ 3t=0$ …(4)
$-3x+ z+ 5-5t=0$ …(5)
(4)×5+(5)×3
$5(-2x+ y+ 1+ 3t)+ 3(-3x+ z+ 5-5t)=0$
$-19x+ 5y+ 3z+ 20=0$ …（答）

【問題3.1】　

　直線 $\frac{x+ 1}{3}=\frac{y-1}{2}=\frac{z-2}{4}$ と点 $P_0(0,\hspace{2}1,\hspace{2}2)$ を含む平面の方程式を求めてください．

解答を見る解答を隠す

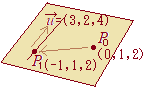直線の方程式を媒介変数表示で表すと

$x=3t-1$
$y=2t+1$
$z=4t+2$
$t=0$のとき点$P_1(-1,1,2)$･･･(1)
$t=1$のとき点$P_2(2,3,6)$･･･(2)
これらと与えられた点$P_0(0,1,2)$･･･(3)の3点を通る平面の方程式を
$ax+by+cz+d=0$
とおいて，未定係数$a,b,c,d$を求める.
(1)により，$-a+b+2c+d=0$･･･(4)
(2)により，$2a+3b+6c+d=0$･･･(5)
(3)により，$b+2c+d=0$･･･(6)

(5)−(4)
$3a+2b+4c=0$･･･(7)
(5)−(6)
$2a+2b+4c=0$･･･(8)

(7)−(8)
$a=0,\hspace{5px}2b+4c=0$
すなわち
$a=0,\hspace{5px}b=-2c$･･･(9)
(9)を(6)に代入する
$d=0$･･･(10)
(9)(10)より
$-2cy+cz=0$
すなわち
$z=2y$･･･(答)

【問題3.2】　

　直線 $\frac{x-3}{2}=\frac{y-4}{3}=\frac{z+ 1}{-1}$ と点 $P_0(-1,\hspace{2}2,\hspace{2}3)$ を含む平面の方程式を求めてください．

解答を見る解答を隠す

$5x-2y+4z-3=0$･･･（答）

4.　直線1を含み直線2と平行な平面の方程式

【例題4】

直線 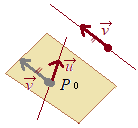$\frac{x-1}{3}=\frac{y+ 1}{-2}=z-3$ を含み，直線 $x+ 2=\frac{y-2}{3}=\frac{z+ 1}{-2}$ と平行な平面の方程式を求めてください．

（解答）
点$P_0(1,-1,3)$を通り，２つのベクトル$\vec{u}=(3,-2,1),\vec{v}=(1,3,-2)$で張られる平面を考える
$\vec{x}=\overrightarrow{\rm{OP_0}}+s\vec{u}+t\vec{v}$
とおける
$(x,y,z)=(1,-1,3)+s(3,-2,1)+t(1,3,-2)$

$x=1+3s+t$･･･(1)
$y=-1-2s+3t$･･･(2)
$z=3+s-2t$･･･(3)
(1)(2)(3)から$s,t$を消去して$x,y,z$の方程式にする
(3)より
$s=z-3+2t$
これを(1)(2)に代入
$x=1+3(z-3+2t)+t$
$=-8+3z+7t$･･･(4)
$y=-1-2(z-3+2t)+3t$
$=5-2z-t$･･･(5)
(4)+7×(5)により$t$を消去
$x+7y=27-11z$
$x+7y+11z=27$･･･（答）

【問題4.1】　

直線 $\frac{x-1}{2}=y+ 2=\frac{z}{3}$ を含み，直線 $\frac{1-x}{3}=\frac{y+ 1}{2}=z-2$ と平行な平面の方程式を求めてください．

解答を見る解答を隠す

$5x+ 11y-7z+ 17=0$ …（答）

【問題4.2】　

直線 $\frac{x+ 1}{-1}=\frac{y+ 3}{2}=\frac{z-2}{3}$ を含み，直線 $x=\frac{y-1}{3}=-z-4$ と平行な平面の方程式を求めてください．

解答を見る解答を隠す

$-11x+ 2y-5z+ 5=0$ …（答）

【問題4.3】　

交わる２直線 $x-1=\frac{y-2}{-1}=\frac{z-3}{2}$ , $\frac{x-2}{2}=y-1=\frac{z-5}{3}$ を含む平面の方程式を求めてください．

解答を見る解答を隠す

点 $(1,\hspace{2}2,\hspace{2}3)$ を通り，２つのベクトル $\vec{l_1}=(1,\hspace{2}-1,\hspace{2}2)$ , $\vec{l_2}=(2,\hspace{2}1,\hspace{2}3)$ で張られる平面を求めるとよいから，解き方としては前問と同じになる．
$5x-y-3z+ 6=0$ …（答）

（別解）
点 $(2,\hspace{2}1,\hspace{2}5)$ を通り，２つのベクトル $\vec{l_1}=(1,\hspace{2}-1,\hspace{2}2)$ , $\vec{l_2}=(2,\hspace{2}1,\hspace{2}3)$ で張られる平面と考える
$5x-y-3z+ 6=0$ …（答）

【問題4.4】　

交わる２直線 $\frac{x+ 1}{2}=\frac{y-1}{3}=\frac{z+ 2}{-1}$ , $\frac{x-2}{-1}=\frac{y-2}{2}=\frac{z+ 8}{5}$ を含む平面の方程式を求めてください．

解答を見る解答を隠す

$17x-9y+ 7z+ 40=0$ …（答）

5.　直線を含み平面に垂直な平面の方程式

【例題5】

直線 $\frac{x+ 1}{3}=\frac{y-1}{2}=\frac{z-2}{4}$ を含み，平面 $x+ 2y+ 3z+ 4=0$ に垂直な平面の方程式を求めてください．

（解答）
　平面 $x+ 2y+ 3z+ 4=0$ に垂直であるから，平面 $x+ 2y+ 3z+ 4=0$ の法線ベクトル $\vec{u}=(1,\hspace{2}2,\hspace{2}3)$ と平行になる．
　点 $(-1,\hspace{2}1,\hspace{2}2)$ を通り，２つのベクトル $\vec{u}=(3,\hspace{2}2,\hspace{2}4)$ ， $\vec{v}=(1,\hspace{2}2,\hspace{2}3)$ で張られる平面を求める．
$(x,y,z)=(-1,1,2)+s(3,2,4)+t(1,2,3)$

$x=-1+3s+t$･･･(1)
$y=1+2s+2t$･･･(2)
$z=2+4s+3t$･･･(3)
(1)より$t=x+1-3s$として(2)(3)に代入
$y=1+2s+2(x+1-3s)=3+2x-4s$･･･(4)
$z=2+4s+3(x+1-3s)=5+3x-5s$･･･(5)
(4)×5+(5)×4
$5y-4z=-5-2x$･･･(4)
$2x+ 5y-4z+ 5=0$ …（答）

【問題5.1】　

直線 $\frac{x+ 1}{2}=\frac{y+ 2}{-1}=\frac{z-1}{3}$ を含み平面 $3x-y+ 2z-10=0$ に垂直な平面の方程式を求めてください．

解答を見る解答を隠す

　点 $(-1,\hspace{2}-2,\hspace{2}1)$ を通り，２つのベクトル $\vec{u}=(2,\hspace{2}-1,\hspace{2}3)$ ， $\vec{v}=(3,\hspace{2}-1,\hspace{2}2)$ で張られる平面を求める．
$(x,y,z)=(-1,-2,1)+s(2,-1,3)+t(3,-1,2)$
以下の変形は前問と同様
$x+ 5y+ z+ 10=0$ …（答）

【問題5.2】　

2点 $P_1(x_1,\hspace{2}y_1,\hspace{2}z_1),\hspace{2}P_2(x_2,\hspace{2}y_2,\hspace{2}z_2)$ を通り，平面 $ax+ by+ cz+ d=0$ に垂直な平面の方程式を求めてください．

解答を見る解答を隠す

　点 $(x_1,\hspace{2}y_1,\hspace{2}z_1)$ を通り，２つのベクトル $\vec{u}=(x_2-x_1,\hspace{2}y_2-y_1,\hspace{2}z_2-z_1)$ ， $\vec{n}=(a,\hspace{2}b,\hspace{2}c)$ で張られる平面を求める．
（中略）
$\{c(y_2-y_1)-b(z_2-z_1)\}(x-x_1)$
$-\{c(x_2-x_1)-a(z_2-z_1)\}(y-y_1)$
$+\{b(x_2-x_1)-a(y_2-y_1)\}(z-z_1)=0$ …（答）

【問題5.3】　

2点 $P_1(1,\hspace{2}2,\hspace{2}-3),\hspace{2}P_2(0,\hspace{2}-1,\hspace{2}2)$ を通り，平面 $3x+ 4y-5z+ 6=0$ に垂直な平面の方程式を求めてください．

解答を見る解答を隠す

上記の問題5.2の結果に代入すれば求まる
$x-2y-z=0$ …（答）

6.　直線と平面がなす角

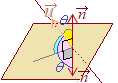　直線の方向ベクトルが $\vec{u}$ ，平面の法線ベクトルが $\vec{n}$ であるとき，これら２つのベクトルのなす角を $\theta$ ，直線と平面がなす角を $\phi$ とすると，
ア）　図中に黄色で示したように $0\underline{\le}\theta\underline{\le}\frac{\pi}{2}$ となるときは，直線と平面のなす角 $\phi$ は，水色で示した角 $\frac{\pi}{2}-\theta$ に等しい．
イ）　図中に桃色で示したように $\frac{\pi}{2}\underline{\le}\theta\underline{\le}\pi$ となるときは，直線と平面のなす角 $\phi$ は，水色で示した角 $\theta-\frac{\pi}{2}$ に等しい．
$\cos\theta=\frac{\vec{u}\cdot\vec{n}}{\left|\vec{u}\right|\cdot\left|\vec{n}\right|}$
であるから，
$\sin\phi=\frac{\left|\vec{u}\cdot\vec{n}\right|}{\left|\vec{u}\right|\cdot\left|\vec{n}\right|}$

【例題6】

直線 $x-1=\frac{y}{2}=z+ 1$ と平面 $2x+ y-z+ 3=0$ がなす角を求めてください．

（解答）
直線の方向ベクトル $\vec{u}=(1,\hspace{2}2,\hspace{2}1)$ ，平面の法線ベクトル $\vec{n}=(2,\hspace{2}1,\hspace{2}-1)$ がなす角は
$\cos\theta=\frac{\vec{u}\cdot\vec{n}}{\left|\vec{u}\right|\cdot\left|\vec{n}\right|}=\frac{2+ 2-1}{\sqrt{6}\cdot\sqrt{6}}=\frac{1}{2}$
$\theta=\frac{\pi}{3}$
であるから，
直線と平面のなす角は $\phi=\frac{\pi}{2}-\frac{\pi}{3}=\frac{\pi}{6}$ …[高校の答え]
（大学では， $\frac{\pi}{6}$ または $\frac{5}{6}\pi$ を解答とすることもある［2つ答える］）

【問題6.1】　

直線 $\frac{x+ 1}{5}=\frac{y-1}{3}=\frac{z-2}{4}$ と平面 $2x-y+ 2z-3=0$ がなす角を求めてください．

解答を見る解答を隠す

直線の方向ベクトル $\vec{u}=(5,\hspace{2}3,\hspace{2}4)$ ，平面の法線ベクトル $\vec{n}=(2,\hspace{2}-1,\hspace{2}2)$ がなす角は
$\cos\theta=\frac{\vec{u}\cdot\vec{n}}{\left|\vec{u}\right|\cdot\left|\vec{n}\right|}=\frac{10-3+ 8}{5\sqrt{2}\cdot 3}=\frac{1}{\sqrt{2}}$
$\theta=\frac{\pi}{4}$
であるから，
直線と平面のなす角は $\phi=\frac{\pi}{2}-\frac{\pi}{4}=\frac{\pi}{4}$ …[高校の答え]
（大学では， $\frac{\pi}{4}$ または $\frac{3}{4}\pi$ を解答とすることもある［2つ答える］）

○===メニューに戻る