|
ЃҰ–і—қЉЦђ”‚М“±ЉЦђ” Ѓ¦Ѓ@‘O’с‚Ж‚И‚йҺ–•ү ЃE–і—қЉЦђ”‚М“±ЉЦђ”‚НЃCҚ‚ҚZ‚Мђ”ЉwIII‚Й“oЏк‚µ‚Ь‚·ЃB ЃEЃu”ч•Ғ‚·‚йЃv‚ЖЃu“±ЉЦђ”‚р‹Ѓ‚Я‚йЃv‚Ж‚Н“Ү‚¶€У–Ұ‚Е‚·ЃB ЃE–і—қЉЦђ”‚М“±ЉЦђ”‚НЃC–і—қЉЦђ”‹y‚С“±ЉЦђ”‚Ғ’и‹`‚і‚к‚й‚Ж‚±‚л‚Е‚М‚ЭҚl‚¦‚Ь‚·ЃB’КЏнЃг‚М’†‚Ғ‚O€ИЏг‚Е‚ ‚й‚±‚ЖЃC(•Ғ•к‚Ғ‚ ‚й‚Ж‚«‚Н)•Ғ•к‚Ғ0‚Е‚И‚ұ‚±‚Ж‚И‚З‚Ғ‘O’с‚Е‚·‚ҒЃC“Б‚Й’f‚з‚ё‚»‚к‚з‚МЏрЊЏ‚р–һ‚Ң‚µ‚Д‚ұ‚й‚Ж‚±‚л‚Е‚М‚ЭҚl‚¦‚Ь‚·ЃB |
|
|
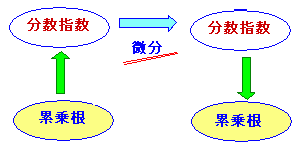
ЃmЉо–{Ѓn
|
—б‘и1
Ѓm“љ€Д—бЃn  |



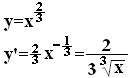 ЃEЃEЃE“љ
ЃEЃEЃE“љ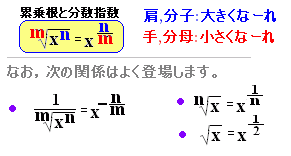
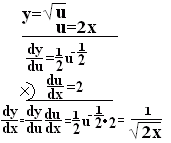 ӨӨӨ“љ
ӨӨӨ“љ
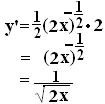 ӨӨӨ“љ
ӨӨӨ“љ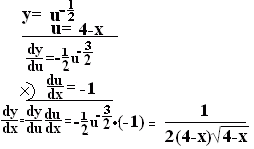 ӨӨӨ“љ
ӨӨӨ“љ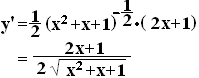 ӨӨӨ“љ
ӨӨӨ“љ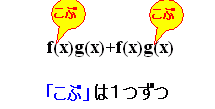
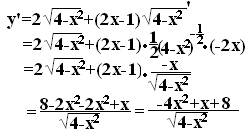 ӨӨӨ“љ
ӨӨӨ“љ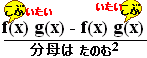
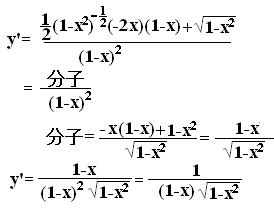 ӨӨӨ“љЃ@Ѓ@
ӨӨӨ“љЃ@Ѓ@