|
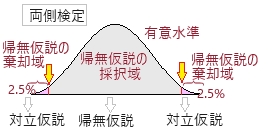
���ȒP�ȗ�ŃC���[�W���(1)��
�y���1�z
�i�l�����j�@10�~�ʂ�10���āC�\�i  �j���i �j���i �j���e�X����o�邩���ׂ��Ƃ���C�\��9��C����1��ł������D �j���e�X����o�邩���ׂ��Ƃ���C�\��9��C����1��ł������D�@����10�~�ʂ́C�\���o�₷���ƌ����邩�H�������C����������Ă��ĕ\���������m��0.5�ŏo��10�~�ʂ�10�����Ƃ��C
��1 �u����10�~�ʂ́C����������Ă��āC1�����Ƃ��ɕ\���o��m����0.5�v���Ɖ��肷��D�i����� ��2 ����ɑ��āC�u����10�~�ʂ͕\���o�₷���v�Ƃ����咣��
�i���l1�j
��3 10�~�ʂ�����������Ă���Ƃ����A�������̂��ƂŁC�u�߂����ɋN����Ȃ��Ɣ��f�ł����ƂȂ�m���v�i�����������@��������͔w���@�ɂ���čs���C����咣�i�Η������j���q�ׂ����Ƃ��ɁC�����ł͂Ȃ��ꍇ�Ɂi�A��������O��Ƃ����ꍇ�Ɂj������������=�߂����ɋN����Ȃ��悤�Ȏ��ɂȂ�Ƃ������Ƃ��������Ƃɂ���āC�A��������ے肵�āC�Η������̐������咣����Ƃ����_�@���Ƃ�D �@���Ȃ킿�C��������ɂ����āC�_���쐬�ҁC�҂����������̂͑Η������ŁC���̂��߂ɁC���������Ȃ���=�A������������Ă����ے肷��Ƃ�����肭�ǂ�������������. |
�i���l2�j
�@�ώ@������̌��ʂv�f�[�^�Ƃ��Ă܂Ƃ߂�Ƃ��C�L�Ӑ����Ƃ��ẮC�قƂ�ǂ̏ꍇ0.05�i5%�j���p������D 95% : 5%=19 : 1 �ɓ��ʂȗ��_�I�Ӗ�������킯�ł͂Ȃ����C���v�f�[�^�Ƃ��Ă܂Ƃ߂�Ƃ��́C�قƂ�ǂ̏ꍇ�C0.05�i5%�j���g����D���ɁC0.1(=10%), 0.01(=1%)�Ȃǂ��p�����邱�Ƃ����邪�C����炪�P�Ƃŗp�����邱�Ƃ͏��Ȃ��C0.05�ɉ����ĎQ�l�Ƃ��ď�����邱�Ƃ������D 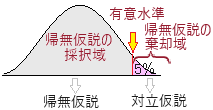 ���̊m���́C�L�Ӑ��������������D���Ȃ킿�C����Ȃ��Ƃ͂߂����ɋN����Ȃ��͂����ƌ�����D �����ŁC�A�����������p����C�Η����������藧�C���Ȃ킿�C�u����10�~�ʂ͕\���o�₷���v�Ɣ��f�ł���D
�i���l3�j
�@�A�������Ƃ����p���́C�ς�����p��ł��邪�C�A�����������藧���Ă��܂�����C�\���̏o��m���ɍ����Ȃ����ƂɂȂ�D���Ȃ킿�u�����Ȃ����Ƃ����肷�邩��A�������ƌĂ���v(*)�D �@�Ȃ��C���̗p��͉�������̍��ڂ��w�ԂƂ��ɕK���o�ꂷ��̂ŁC�e���ʼn��g���Ă݂āC�������ꂽ�����悢����M�҂́C���ߕ������Ƃ��Ɂu���ꂪ���藧������C�����Ȃ��Ȃ�D���ɋA����=�������ɍs������I�V�}�C���v�Ƃ����Ӗ����Ǝv���Ă������C�����炸�Ƃ����ǂ������炸���ȁD (*)�u�������v�w�v�iP.G.�z�[�G���� / ���W���� / �|���� p.174�j
�i���l4�j
�@�L�Ӑ����͊m���ŁC�قƂ�ǂ̏ꍇ0.05(5%)��p����D�L�Ӑ�������ɓ��Ă͂߂āC�Ⴆ�u�\��9��ȏ�o�邱�Ɓv�Ƃ����悤�ɔ͈͂ɂ������̂����p���ƌĂ��D �@�����I�ɏq�ׂ�Ƃ��́u�A�����������p�����v�u�A�����������p������v�Ƃ���������������D |
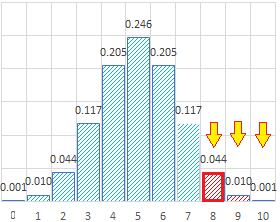
 �j��5��o���D
�j��5��o���D