|
■角の二等分線と補助線
【比例←相似図形】
平行線の性質(相似)を利用すると,比例の関係を示すことができます. 例えば右図1において
|
図1
 |
|
【角の二等分線の性質】
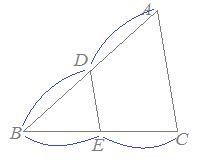
※この定理は中学校では習いませんので,中学生に対して「覚えなさい」とか「この問題がよく出る」というようなことは言えませんが,ヒントを示してこの定理を誘導する問題ならありえます.△ABCにおいて右図2のように線分ADが∠Aを二等分しているとき, 角の二等分線の性質は高校数学Aの教科書で登場しますが,数学Aの中で平面幾何を選択することはほとんどないため,この定理に接する機会はめったにありません.
≪注意すべきこと≫
右図2ではDはBCの中点ではありません.右図2のように頂点Aが右寄りになっているとき∠BAD=∠DACとしたとき(角の二等分線を引いたとき)には,BDの方がDCよりも長くなります. まずはじめに,この頁ではDがBCの中点になっている話をしているのではなく,ADが∠Aの二等分になっている場合を取り扱っていることに注意してください. △ABCが二等辺三角形になるような特別な場合を除けば,一般にはBD≠DCになり,角の二等分線ADによって辺BCは二等分されません. |
図2
 |
|
例1
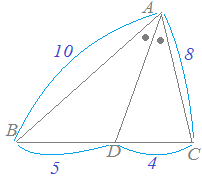
(証明)△ABCにおいて線分ADが∠Aを二等分しているとき,右図3のようにCからDAに平行線を引きBAの延長との交点をEとおくと,BD:DC=BA:ACとなることを証明することができます. AD//ECだから,平行線の性質(または相似図形の性質)により BD:DC=BA:AE…(1) また,次のようにしてAE=ACを示すことができる.
仮定によりADは∠BACの二等分線だから
(1)(6)より∠BAD=∠DAC…(2) 平行線の同位角は等しいから ∠BAD=∠AEC…(3) 平行線の錯角は等しいから ∠DAC=∠ACE…(4) (2)(3)(4)より ∠AEC=∠ECA…(5) △ACEは両底角が等しいから二等辺三角形で AE=AC…(6) BD:DC=BA:AC…(証明終り) |
図3
【要約】
|
|
問1
採点するやり直すHelp
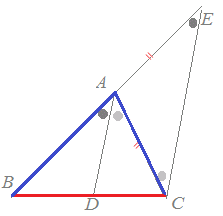
△ABCにおいて線分ADが∠Aを二等分しているとき,右図4のようにBからDAに平行線を引きCAの延長との交点をEとおくと,BD:DC=BA:ACとなることを証明することができます.次の空欄を埋めてください. |
図4
 |
|
問2
採点するやり直すHelp
△ABCにおいて線分ADが∠Aを二等分しているとき,右図5のようにCからABに平行線を引きADの延長との交点をEとおくと,BD:DC=BA:ACとなることを証明することができます.次の空欄を埋めてください. |
図5
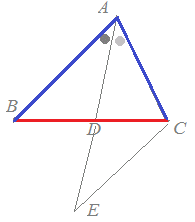 |
|
問3
採点するやり直すHelp
△ABCにおいて∠Aの外角の二等分線が辺BCの延長と交わる点をDとするとき,右図6のようにDからCAに平行線を引きBAの延長との交点をEとおくと,BD:DC=BA:ACとなることを証明することができます.次の空欄を埋めてください. |
図6
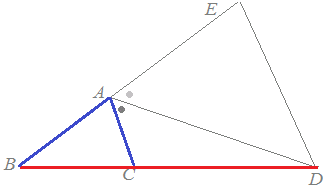 |
|
問4
採点するやり直すHelp
△ABCにおいて∠Aの外角の二等分線が辺BCの延長と交わる点をDとするとき,右図7のようにCからABに平行線を引きADとの交点をEとおくと,BD:DC=BA:ACとなることを証明することができます.次の空欄を埋めてください. |
図7
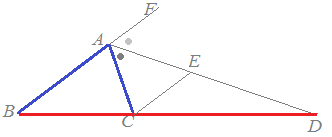 |
|
問5
採点するやり直すHelp
△ABCにおいて∠Aの外角の二等分線が辺BCの延長と交わる点をDとするとき,右図8のようにCからADに平行線を引きABとの交点をEとおくと,BD:DC=BA:ACとなることを証明することができます.次の空欄を埋めてください. |
図8
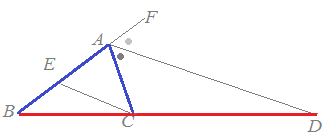 |
|
【証明の進め方】 ここまでは実際の証明方法を学んできましたが,慣れてくれば鉛筆を持つ前に全体の見通しを立てることが重要です. 問題 左欄のように補助線をひいて証明を行うためには,どのように証明を進めたらよいでしょうか.(証明方法はいろいろ考えられますが,ここでは右欄の方法のうちでよいものを選んでください.) (はじめに左欄から1つ選び,続いてこれに対応する進め方を右欄から選んでください.) Help 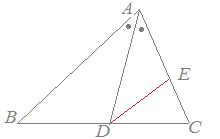 △ABCにおいて線分ADが∠Aを二等分しているとき,BD:DC=BA:ACとなることを証明するために,図のようにDからBAに平行線を引きACとの交点をEとおいたとき △ABCにおいて線分ADが∠Aを二等分しているとき,BD:DC=BA:ACとなることを証明するために,図のようにDからBAに平行線を引きACとの交点をEとおいたとき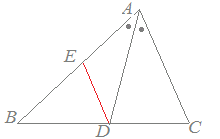 △ABCにおいて線分ADが∠Aを二等分しているとき,BD:DC=BA:ACとなることを証明するために,図のようにDからCAに平行線を引きABとの交点をEとおいたとき △ABCにおいて線分ADが∠Aを二等分しているとき,BD:DC=BA:ACとなることを証明するために,図のようにDからCAに平行線を引きABとの交点をEとおいたとき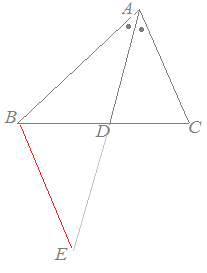 △ABCにおいて線分ADが∠Aを二等分しているとき,BD:DC=BA:ACとなることを証明するために,図のようにBからACに平行線を引きADの延長との交点をEとおいたとき △ABCにおいて線分ADが∠Aを二等分しているとき,BD:DC=BA:ACとなることを証明するために,図のようにBからACに平行線を引きADの延長との交点をEとおいたとき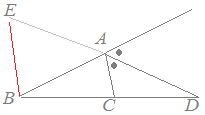 △ABCにおいて∠Aの外角の二等分線と線分BCの延長との交点をDとするとき,BD:DC=BA:ACとなることを証明するために,図のようにBからCAに平行線を引きADの延長との交点をEとおいたとき △ABCにおいて∠Aの外角の二等分線と線分BCの延長との交点をDとするとき,BD:DC=BA:ACとなることを証明するために,図のようにBからCAに平行線を引きADの延長との交点をEとおいたとき |
【考え方のポイント】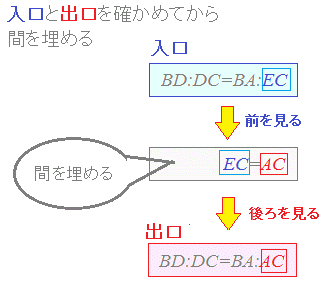
相似図形の性質からBD:DC=BE:ACを示し,
二等辺三角形の性質からBE=BAを示せば, BD:DC=BA:ACが証明できる.
相似図形の性質からBD:DC=EA:ACを示し,
二等辺三角形の性質からEA=BAを示せば, BD:DC=BA:ACが証明できる.
相似図形の性質からBD:DC=BA:ECを示し,
二等辺三角形の性質からEC=ACを示せば, BD:DC=BA:ACが証明できる.
相似図形の性質からBD:DC=AE:ECを示し,
二等辺三角形の性質からAE=DEを示せば, BD:DC=DE:ECが示せて, さらに相似図形の性質からBD:DC=BA:ACが証明できる.
相似図形の性質からBD:DC=BE:EAを示し,
二等辺三角形の性質からEA=EDを示せば, BD:DC=BE:EDが示せて, さらに相似図形の性質からBD:DC=BA:ACが証明できる. |