【問題6.1】
ねじれの位置にある2直線  \( \displaystyle \frac{x-5}{2}=y-4=z-2 \) \( \displaystyle \frac{x-5}{2}=y-4=z-2 \)と
 \( \displaystyle \frac{x+ 1}{-5}=\frac{y-3}{2}=\frac{z-3}{-4} \) \( \displaystyle \frac{x+ 1}{-5}=\frac{y-3}{2}=\frac{z-3}{-4} \)との距離を求めてください.
解答を見る解答を隠す
(解答)
2直線の方向ベクトルは各々 ,\hspace{2}\vec{l_2}=(-5,\hspace{2}2,\hspace{2}-4)&chs=190x23) \( \displaystyle \vec{l_1}=(2,\hspace{2px}1,\hspace{2px}1),\hspace{2px}\vec{l_2}=(-5,\hspace{2px}2,\hspace{2px}-4) \) \( \displaystyle \vec{l_1}=(2,\hspace{2px}1,\hspace{2px}1),\hspace{2px}\vec{l_2}=(-5,\hspace{2px}2,\hspace{2px}-4) \)
) \( \displaystyle \vec{l_1}\times\vec{l_2}=(-6,\hspace{2px}3,\hspace{2px}9) \) \( \displaystyle \vec{l_1}\times\vec{l_2}=(-6,\hspace{2px}3,\hspace{2px}9) \)
直線上の2点 ,\hspace{2}P_2(-1,\hspace{2}3,\hspace{2}3)) \( \displaystyle {\rm P_1}(5,\hspace{2px}4,\hspace{2px}2),\hspace{2px}P_2(-1,\hspace{2px}3,\hspace{2px}3) \) \( \displaystyle {\rm P_1}(5,\hspace{2px}4,\hspace{2px}2),\hspace{2px}P_2(-1,\hspace{2px}3,\hspace{2px}3) \)を結ぶベクトルは
) \( \displaystyle \overrightarrow{{\rm P_1P_2}}=(-6,\hspace{2px}-1,\hspace{2px}1) \) \( \displaystyle \overrightarrow{{\rm P_1P_2}}=(-6,\hspace{2px}-1,\hspace{2px}1) \)
\right|}{\left|\vec{l_1}\times\vec{l_2}\right|}=\frac{|36-3%2B 9|}{\sqrt{36%2B 9%2B 81}}=\frac{42}{\sqrt{126}}) \( \displaystyle d=\frac{\left|\overrightarrow{{\rm P_1P_2}}\cdot(\vec{l_1}\times\vec{l_2})\right|}{\left|\vec{l_1}\times\vec{l_2}\right|}=\frac{|36-3+ 9|}{\sqrt{36+ 9+ 81}}=\frac{42}{\sqrt{126}} \) \( \displaystyle d=\frac{\left|\overrightarrow{{\rm P_1P_2}}\cdot(\vec{l_1}\times\vec{l_2})\right|}{\left|\vec{l_1}\times\vec{l_2}\right|}=\frac{|36-3+ 9|}{\sqrt{36+ 9+ 81}}=\frac{42}{\sqrt{126}} \)
 \( \displaystyle =\frac{42}{3\sqrt{14}}=\sqrt{14} \) \( \displaystyle =\frac{42}{3\sqrt{14}}=\sqrt{14} \)
(別解)
直線  \( \displaystyle \frac{x-5}{2}=y-4=z-2 \) \( \displaystyle \frac{x-5}{2}=y-4=z-2 \)上の点
 \( \displaystyle {\rm P} \) \( \displaystyle {\rm P} \)を
 \( \displaystyle x_1=2s+ 5 \) \( \displaystyle x_1=2s+ 5 \)
 \( \displaystyle y_1=s+ 4 \) \( \displaystyle y_1=s+ 4 \)
 \( \displaystyle z_1=s+ 2 \) \( \displaystyle z_1=s+ 2 \)
直線  \( \displaystyle \frac{x+ 1}{-5}=\frac{y-3}{2}=\frac{z-3}{-4} \) \( \displaystyle \frac{x+ 1}{-5}=\frac{y-3}{2}=\frac{z-3}{-4} \)上の点
 \( \displaystyle {\rm Q} \) \( \displaystyle {\rm Q} \)を
 \( \displaystyle x_2=-5t-1 \) \( \displaystyle x_2=-5t-1 \)
 \( \displaystyle y_2=2t+ 3 \) \( \displaystyle y_2=2t+ 3 \)
 \( \displaystyle z_2=-4t+3 \) \( \displaystyle z_2=-4t+3 \)
とすると
) \( \displaystyle \overrightarrow{{\rm PQ}}=(-5t-2s-6,\hspace{2px}2t-s-1,\hspace{2px}-4t-s+ 1) \) \( \displaystyle \overrightarrow{{\rm PQ}}=(-5t-2s-6,\hspace{2px}2t-s-1,\hspace{2px}-4t-s+ 1) \)
ここで  \( \displaystyle \overrightarrow{{\rm PQ}}\perp\vec{l_1},\hspace{2px}\overrightarrow{{\rm PQ}}\perp\vec{l_2} \) \( \displaystyle \overrightarrow{{\rm PQ}}\perp\vec{l_1},\hspace{2px}\overrightarrow{{\rm PQ}}\perp\vec{l_2} \)となる
 \( \displaystyle s,\hspace{2px}t \) \( \displaystyle s,\hspace{2px}t \)を求める
 \( \displaystyle \overrightarrow{{\rm PQ}}\perp\vec{l_1} \) \( \displaystyle \overrightarrow{{\rm PQ}}\perp\vec{l_1} \)より
%2B(2t-s-1)%2B(-4t-s%2B 1)=0) \( \displaystyle 2(-5t-2s-6)+(2t-s-1)+(-4t-s+ 1)=0 \) \( \displaystyle 2(-5t-2s-6)+(2t-s-1)+(-4t-s+ 1)=0 \)
 \( \displaystyle -12t-6s-12=0 \) \( \displaystyle -12t-6s-12=0 \)
 \( \displaystyle -2t-s-2=0 \) \( \displaystyle -2t-s-2=0 \)…(1)
 \( \displaystyle \overrightarrow{{\rm PQ}}\perp\vec{l_2} \) \( \displaystyle \overrightarrow{{\rm PQ}}\perp\vec{l_2} \)より
%2B 2(2t-s-1)-4(-4t-s%2B 1)=0&chs=350x19) \( \displaystyle -5(-5t-2s-6)+ 2(2t-s-1)-4(-4t-s+ 1)=0 \) \( \displaystyle -5(-5t-2s-6)+ 2(2t-s-1)-4(-4t-s+ 1)=0 \)
 \( \displaystyle 45t+ 12s+ 24=0 \) \( \displaystyle 45t+ 12s+ 24=0 \)
 \( \displaystyle 15t+ 4s+ 8=0 \) \( \displaystyle 15t+ 4s+ 8=0 \)…(2)
(1)(2)より  \( \displaystyle s=-2,\hspace{2px}t=0 \) \( \displaystyle s=-2,\hspace{2px}t=0 \)
このとき, ,\hspace{2}Q(-1,\hspace{2}3,\hspace{2}3)) \( \displaystyle {\rm P}(1,\hspace{2px}2,\hspace{2px}0),\hspace{2px}{\rm Q}(-1,\hspace{2px}3,\hspace{2px}3) \) \( \displaystyle {\rm P}(1,\hspace{2px}2,\hspace{2px}0),\hspace{2px}{\rm Q}(-1,\hspace{2px}3,\hspace{2px}3) \)より
 \( \displaystyle {\rm PQ}=\sqrt{4+ 1+ 9}=\sqrt{14} \) \( \displaystyle {\rm PQ}=\sqrt{4+ 1+ 9}=\sqrt{14} \)
|
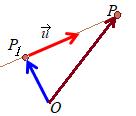 「点P1を通り,方向ベクトル
「点P1を通り,方向ベクトル
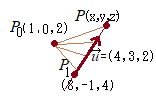 (解答)
(解答) (別解1)
(別解1)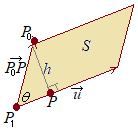 (別解2)
(別解2)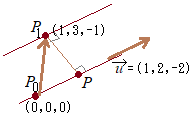 (解答)
(解答)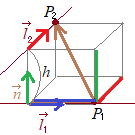 点
点 右図のように直線と
右図のように直線と 2直線のなす角は,2直線の方向ベクトルのなす角で定義される.ねじれの位置にある場合でも2直線のなす角を考えます.
2直線のなす角は,2直線の方向ベクトルのなす角で定義される.ねじれの位置にある場合でも2直線のなす角を考えます.