|
■固有値,固有ベクトルの定義
n次正方行列Aに対して
A=λ (≠)
となるような定数λとベクトル(n次元の列ベクトル)が存在するとき,λをAの固有値といい,をλに属する(に対する)固有ベクトルという.
○ 任意の正方行列Aに対して零ベクトル=は常にA=λを満たすが,このような解(自明解)=は固有ベクトルに含めない.
例1 2次正方行列での例
このように固有ベクトルが零ベクトルでない≠という仮定は本質的なものである. ○ しかし他方では,固有値がλ=0となることは,しばしばある.次の例においてはλ=0の固有値が存在する. 例 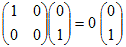 だからλ=0は固有値 だからλ=0は固有値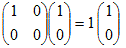 だからλ=1は固有値 だからλ=1は固有値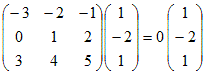 だからλ=0は固有値 だからλ=0は固有値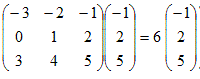 だからλ=6は固有値 だからλ=6は固有値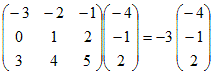 だからλ=−3は固有値 だからλ=−3は固有値
A=
例2 3次正方行列での例
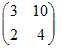 のとき, のとき,
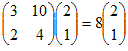 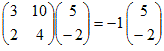
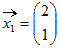 固有値λ2= −1に属する固有ベクトルは 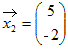
A=
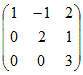 のとき, のとき,
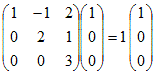 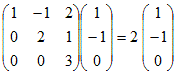 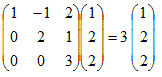
固有値λ1=1に属する固有ベクトルは 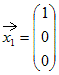 固有値λ2=2に属する固有ベクトルは 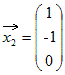 固有値λ3=3に属する固有ベクトルは 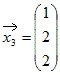 |
|
○ あるベクトルが固有ベクトルであるとき,その定数倍(0倍以外)はすべて固有ベクトルとなる.
A=λ → A(k)=λ(k)
(3次元を例にとると)1つの固有ベクトルが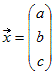 のとき, のとき,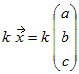 (kは0以外の数)の形でその方向のすべての固有ベクトルを表すことができる. (kは0以外の数)の形でその方向のすべての固有ベクトルを表すことができる.そこで,固有値と固有ベクトルを答えるとき,固有値は数値で答え,固有ベクトルは 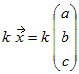 (kは0以外の数)の形で答えるとよい. (kは0以外の数)の形で答えるとよい.
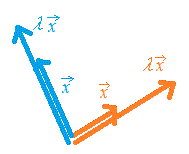
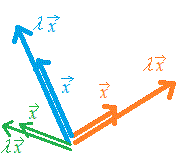
○ 固有ベクトルの図形的意味 ≠で
A=λ
となるとき,右辺はベクトルの定数倍だから,固有ベクトルとは行列Aによって
方向が変わらないベクトル
ということになる.(固有値が1でない限り大きさは変わる.固有値が負の数のときは逆向きになる・・・同じ向きと逆向きとを合わせて同じ方向というので,方向は変わらない.)2次元の場合,平面上のほとんどのベクトルはこのような性質をもたないが,2つの直線上にあるベクトルだけは方向が変わらない固有ベクトルとなる.
  ○ 原点のまわりに角度Θだけ回転することを表す行列 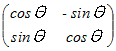 では,実数の固有値はない.(固有値は虚数になる.)このような場合には,x-yの実数平面上には方向の変わらないベクトルはない. では,実数の固有値はない.(固有値は虚数になる.)このような場合には,x-yの実数平面上には方向の変わらないベクトルはない.
|