|
=== �ǎ҂��z�F��ύX�������ꍇ ===
���O���̐F��ς���ɂ́C���̐F���N���b�N
== �Z���^�[����.��B.����(2013�`) ==
�y2013�N�x�Z���^�[����.���w�U�B�z��3��i�I����j
(1)�@����{pn}�͎������Ƃ���B ����{pn}�̈�ʍ��ƁC���������n���܂ł̘a�����߂悤�B�܂��C�@����
�ƂȂ�̂ŁC����{pn}�̈�ʍ���
�ł���B���������āC���R��n�ɑ���
�ł���B |
�����ǂ�
(1)
�y�萔�W���̓ԑQ�����˓��䐔��z
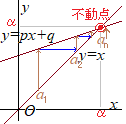
�@�萔�W���̓ԑQ����an+1=pan+q�i�������Cp, q�͒萔�j���C���_�̈ړ�{an−α}�ɂ��C{an−α}�����䐔��ƂȂ�悤�ɒ萔α���߂āC���䐔��̈�ʍ����猳�̐���{an}�̈�ʍ������߂���@
�����������̉��i�s���_�jα�𗘗p������@
�s�p��t
• �ԑQ�����Fan+1=pan+q����@ • �����������Fα=pα+q����A
�@�ɂ����āC
• �s���_�F�����������̉�α����B�̂��� |
 �i�Q�l�j
�i�Q�l�j