|
=== 読者が配色を変更したい場合 ===
◎外側の色を変えるには,次の色をクリック
このページの「マイナーチェンジありカバー版」「広告なし」「パソコン用」ページ
(グーグルブロガー版)は,こちら⇒ == センター試験.数Ⅱ微積(2013~) ==
【2013年度センター試験.数学Ⅱ・B】第2問(必答問題)
aを正の実数として,xの関数f(x)を
f(x)=x3−3a2x+a3
とする。関数y=f(x)は,x=アイで極大値ウaエをとり,x=オで極小値カaキをとる。このとき,2点 と原点を通る放物線
y=クx2−ケaコx
をCとする。原点におけるCの接線ℓの方程式は
y=サシaスx
である。また,原点を通りℓに垂直な直線mの方程式は
である。 |
解説を読む
f’(x)=3x2−3a2=3(x+a)(x−a)
a>0だから,増減表は次のようになる.
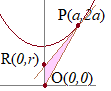
x=aのとき,極小値−a3をとる→オ,カ,キ 3点O(0, 0), P(−a, 3a3), Q(a, −a3)を通る放物線の方程式を y=Ax2+Bx+C とおく. O(0, 0)を通るから C=0・・・(#1) P(−a, 3a3)を通るから 3a3=Aa2−Ba+C・・・(#2) Q(a, −a3)を通るから −a3=Aa2+Ba+C・・・(#3) (#1)(#2)(#3)より A=a, B=−2a2, C=0 y=ax2−2a2x→ク,ケ,コ ⇒(#4)放物線C (#4)を微分すると y'=2ax−2a2 x=0のとき,y'=−2a2だから,接線ℓの方程式は y=−2a2x→サシ,ス 垂線mの方程式は
♪∀~勝手に批評~個人の感想~∅♥
ここまでは,誰でもできる.受験生間の差は出ない. |
 (2)
(2) 〔2〕
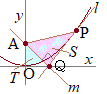
〔2〕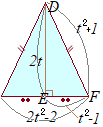 右図の直角三角形
右図の直角三角形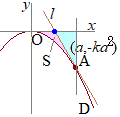
 点
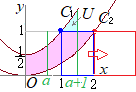
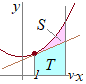
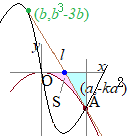
点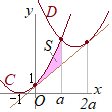 二つの放物線
二つの放物線