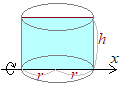
|
== ���̂̑̐� ==
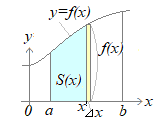 �i�ʐς̕��K�j
�i�ʐς̕��K�j�@a��x��b�̋�Ԃ�x����y=f(x)�Ƃň͂܂��}�`�̖ʐς��C�c�̒���f(x)�̐ϕ��ŕ\���ꂽ�����U��Ԃ��Ă݂܂��D �@a����x�܂łɕ`�����}�`�̖ʐς�S(x)�Ƃ����� �@x���킸������x�������������Ƃ��C������ʐς͉��F�Ŏ����������`�̖ʐρC���Ȃ킿�c�̒���f(x)�Ɖ��̒�����x�̐ςɂقړ������Ȃ�܂��D ��S(x)��f(x)��x ���������� �@������x������Ȃ��O�ɋ߂Â���ƁC���̋Ɍ��͋ߎ��l�ł͂Ȃ����m��f(x)�ɓ������ƌ��Ȃ��܂��D �@���̂��̂����ڂɂ͕�����Ȃ��Ă��C���̔�����������C�ϕ��ɂ���Ėʐ�S(x)�����܂�܂��D �@a��x��b�̋�Ԃł�
�ʐς����߂����Ƃ�
�� �ʐς̔��� |
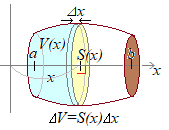 �i�̐ς̌v�Z�j
�i�̐ς̌v�Z�j�@���̂̑̐ς����߂�ɂ́C�̐ς̔������f�ʐςɂȂ邱�Ƃ𗘗p���܂��D �@���Ȃ킿�C���[a������Wx�܂ł̋�Ԃɂ���̐ς�x�̊��Ƃ���V(x)�ŕ\���Cx�ɂ�����f�ʐς�S(x)�Ƃ����܂��D �@��ŕ��K�����ʐς̋��ߕ��Ɠ��l�ɂ��� ��V(x)��S(x)��x ��������܂��D
�̐ς����߂����Ƃ�
�� �̐ς̔���V’(x)���f�ʐ�S(x)�ɂȂ�̂�V�͒f�ʐς̐ϕ��ŋ��߂��� 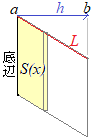 ���i���Ӂj
���i���Ӂj�@���s�l�ӌ`�̖ʐς� 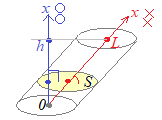 �@���l�ɂ��āC�̐ς̌v�Z�ɂ����Ă��C�u�f�ʐςƍ��W��x�Ƃ��w�����x�ɂȂ��Ă��Ȃ���Ȃ�܂���v�D
�@���l�ɂ��āC�̐ς̌v�Z�ɂ����Ă��C�u�f�ʐςƍ��W��x�Ƃ��w�����x�ɂȂ��Ă��Ȃ���Ȃ�܂���v�D�@�����łȂ���C ��V(x)��S(x)��x�����藧�����Ȃ��Ȃ�C��ŏq�ׂ��O����܂��D |
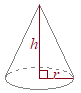
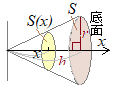 �E�̂悤�ɒ�ʂɐ�����
�E�̂悤�ɒ�ʂɐ�����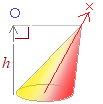 ���E�}�̂悤�ȎO�p�X�q�ł����Ă��C
���E�}�̂悤�ȎO�p�X�q�ł����Ă��C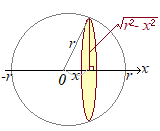 �@�E�}�̂悤�ɁC���a�ɉ�����
�@�E�}�̂悤�ɁC���a�ɉ�����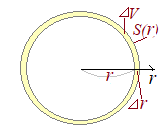 �@�\�ʐς����߂�ɂ������āC���a
�@�\�ʐς����߂�ɂ������āC���a
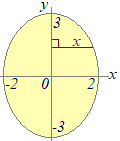
 �~�̖ʐ�
�~�̖ʐ�
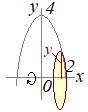 (1)
(1) 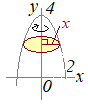 (2)
(2) 

 �i�j
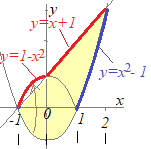
�i�j ����}�`�̈����Z��
����}�`�̈����Z�� �E�}�̐ԂŎ����������O���̐��ŁC�Ŏ����������������ɂȂ���ł��D
�E�}�̐ԂŎ����������O���̐��ŁC�Ŏ����������������ɂȂ���ł��D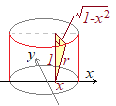 �i�j
�i�j