位置ベクトルの応用

→ 携帯版は別頁 ■　位置ベクトルの応用 ◇公式の要約◇ ２点 A( ) , B( ) を結ぶベクトル →AB は，→AB = −	○補足説明　記号　A( )　は，関数の記号 f(x) とは無関係。平面の座標を表わすときに，「点 A，その座標を (3 , 4) とおく」というのを A(3 , 4) と書くのと同様にして，「点A，その位置ベクトルをとおく」というのを単に，点 A( ) と書く。【注意】　 →AB = − ではない！
２点 A( ) , B( ) の中点 M の位置ベクトルは， =	○補足説明
２点 A( ) , B( ) を結ぶ線分 AB m : n に内分する点 P の位置ベクトルは， =	○補足説明
△ABC の頂点 A,B,C の位置ベクトルを各々，，とすると，△ABC の重心 G の位置ベクトルは， =	○補足説明

■　問題　次の空欄を埋めなさい。
（半角数字［１バイト文字］で答えてください）

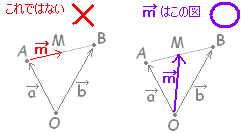
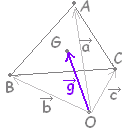
(1)　△ABC の線分 AB,BC,CA の中点を各々 L,M,N とする。△ABC の重心 G と△LMN の重心 G ’ は一致することを証明しなさい。

(証明)

$\vec{g}=\frac{\vec{a}+\vec{b}+\vec{c}}{3}$
$\frac{\vec{a}+\vec{b}}{2},\hspace{5}\frac{\vec{b}+\vec{c}}{2},\hspace{5}\frac{\vec{c}+\vec{a}}{2}$
$\vec{g\apos}=\frac{\frac{\vec{a}+\vec{b}}{2}+\frac{\vec{b}+\vec{c}}{2}+\frac{\vec{c}+\vec{a}}{2}}{3}=\frac{\vec{a}+\vec{b}+\vec{c}}{3}$ →閉じる←

(2)　△ABC 頂点 A,B,C の位置ベクトルを各々 , , とするとき，右の空欄を埋めなさい。

$\vec{p}=\frac{\vec{a}+ 2\vec{b}}{3},\hspace{10}\vec{q}=\frac{\vec{c}+ \vec{a}}{2}$
$\vec{PQ}=\vec{q}-\vec{p}=\frac{\vec{a}-4\vec{b}+ 3\vec{c}}{6}$
→閉じる←

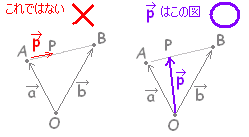
(3)　△ABC と点 P について

→PA+2→PB+3→PC=2→AB

が成り立っているとき，点 P はどのような点か。

$\vec{a}+ 2\vec{b}+ 3\vec{c}-6\vec{p}=2\vec{b}-2\vec{c}$
$\vec{p}=\frac{\vec{a}+\vec{c}}{2}$
中点 →閉じる←

(4)　△ABCと点 P について

2→PA+ 3→PB+ 4→PC=

が成り立っているとき，点 P はどのような点か。

3:2
4:5
→閉じる←

○＝＝メニューに戻る