|
○期待値とは,小中学校で習った平均値のことです. すなわち,表1のように変数x1 ,x2 ,x3 ,...,xNが合計N個あるとき,それらの平均値m (mean value)または期待値E(X)(Expectation)は,変数の合計x1+x2+x3+...+xNをNで割ったものになります. m=
○表2のように確率分布表で表されている場合には m=x1 +x2 +x3 +…+xN …(*1) となって,各々の変数xk (k=1,2,3,...,N)とその確率との積の和になります.
x1+……+x2+……+......+xn+……   f1個f2個(←合計N個) =x1 f1+x2 f2+……+xn fn となるから,平均値は m=…(*2)
=pk (k=1,2,3,...,n)とおくと,平均値は m=E(X)=x1p1+x2p2+x3p3+...+xnpn
【要約】
表1のように,変数x1 ,x2 ,x3 ,...,xNが合計N個あるとき,それらの平均値(期待値)は, m=E(X)=…(1) 表5のように,確率変数x1 , x2 , ...に対応する確率が各々p1 , p2 , ...のとき,平均値(期待値)は m=E(X)=x1 p1+x2 p2+x3 p3+...+xn pn…(2)
 =pkとおく =pkとおく
|
|
(参考)
◎ 平均値(期待値)の長所
平均値は,「真ん中あたりがどこにあるか」を示しており,統計データを集約するときに最も重要なものです.以下に示すように,平均値にも弱点はありますが,ほとんどすべての統計において平均値が使われます.
元の変数x1 ,x2 ,x3 ,...,xNがN個のデータであるのに対して,平均値はただ1個の数値です.だから,元のデータが持っていた情報量がN次元であったのに対して,平均値はたった1次元の情報しか持っていません.これは平均値に限らず,統計データの代表値にはすべて当てはまることですが,平均値という中心付近を表す代表値1つだけでは,元のデータが持っていた「各々の個性」は表現できません.それでも,N個の生のデータを引きずっていく煩わしさよりは,1個の数値で全体の傾向がわかる便利さに目を向けることが重要です.
図1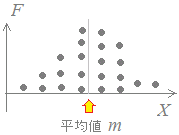
△ 平均値の弱点→別の代表値を使う場合
図3例えば,図2のように,極端値(外れ値)を含むようなデータにおいては,平均値は「順位の中央」からかなり離れた所に来ます.
【例】 アメリカでは,人口の1%の人が富の99%を持っており,残り99%に人が富の1%を分けあっているといわれています.このような場合に,収入の平均値は極端な富豪の収入に引きずられて,庶民の収入とはかけ離れた高い値になります.
【例】 中高生の家庭学習の時間についていえば,2割の子供たちが家庭学習時間の8割を行っていると言われており,家庭学習をほとんどしない子供たちが多くいると言われています.このような場合に,家庭学習時間の平均値は,多くの子供たちの実態からはかけ離れた高い数値になっています. 【例】 多くの集団において遅刻の回数は,そのほとんどを数人の人が計上しており,平均値が多くても,その集団全体の遅刻傾向とは無関係で,特定の個人の傾向を表していることが多いようです. 順位を重視して,上半分と下半分の中央に来る値は「中央値(メジアン)」と呼ばれます. (*2)式を見るとわかるように,平均値の計算においては,すべての変数xkの値が,公平に同じ確率で評価されています.これは,どの値xkが少し変化しても,そのだけ平均値に反映されることを示しています. 例えば,a<b<cでcが極端に大きな外れ値のとき,平均値では =a+b+c となりますが,中央値(メジアン)は =a+b+c=b となって,極端値cが変化しても影響を受けません. このような中央値(メジアン)は「順位の中央」に着目して,上半分と下半分に分けたいときなどに用いられます. 図2  △ 平均値の弱点→別の代表値を使う場合 図3がある商品(例えば靴)のサイズや価格帯と売れ行きを表しているような場合に,平均値付近の商品を品ぞろえしても,対応できません.平均値は「真ん中あたり」を表してはいますが,「最もよく売れるサイズや価格帯」に一致するとは限りません. 頻度が最大となっている(山が一番高い)値を「最頻値(モード)」といい,売れ筋商品を考えるような場合に使われます. 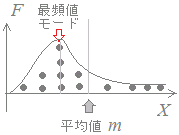 平均値E(X)という1種類の代表値だけでは,元のデータの傾向が表し切れないことに対しては,次に述べる分散V(X)(または標準偏差σ(X))というもう一つの代表値と合わせて2種類の代表値を併用することによって,全体の傾向を表します.(ほとんどの場合,高校でも大学でもこの2つの代表値を使えば十分です.) ◎ データの散らばり方を表す代表値:分散V(X)(または標準偏差σ(X)) 図4 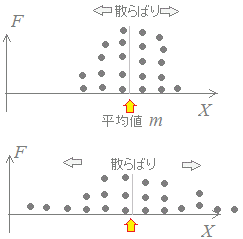 平均値E(X)だけでは区別できない散らばりを表す数字が分散V(X)(または標準偏差σ(X))です. 下の図5においては,AとCは平均値が等しくて,散らばりはCの方が大きくなっています. また,AとBとでは,散らばりが等しく,平均値はBの方が大きくなっています. AとD,BとCでは平均値も散らばりも異なっています. 図5 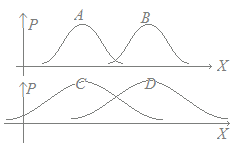 数学の得点は,散らばりが大きく,平均値の辺りに多くの得点が集まっている訳ではないので,その平均値にどれだけの重要性があるのか?と思うこともありますが,逆に,散らばりが大きいということは,個人差が大きいということで,数学の得点を見れば個人差がよく分かることになります.(ここで分かる個人差は理数系の得意不得意です) 
【要約】
N個の変数からなるデータの特徴を幾つかの数値に集約して表すときに,通常2つの数値が使われます.
N個の変数からなるデータの情報量を完全に維持しようとすると,理論上N個の数値が必要となるが,それでは煩わしさが元と同じで集約したことにならない.
N個の変数からなるデータの特徴を数個の数値で「集約」するときに,通常,次の2つが使われます.
◎平均値E(X)
「真ん中あたりがどこにあるか」を示しており,統計データを集約するときに最も重要なもので,ほとんどすべての統計において平均値が使われます.
◎分散V(X)(または標準偏差σ(X))
データの散らばり具合を表しています. |
|
【例題1】
(解答)2つのさいころを同時に投げるとき,出た目の和の期待値を求めてください.
◆ポイント◆ ⇒「期待値」ときたら「確率分布表」を作る!
2つのさいころを同時に投げるとき,目の出方は合計36通りあり,次の表のように
和が2 → 1通り
となるから,確率分布表は次のようになる.和が3 → 2通り … 和が12 → 1通り
E(X)=2×+3×+4×+5×+ 6×+7× +8×+9×+10×+11×+12× =(2+6+12+20+30+42+40+36+30+22+12)=7 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||
 【例題2】 【例題2】袋の中に赤玉が3個,白玉が2個,合計5個の玉が入っているとき,次の各々の場合について,2つの期待値を比較してください. (1) 同時に2個取り出すとき,その中に含まれる赤玉の個数の期待値,白玉の個数の期待値 (2) 1個ずつ2回取り出すとき,赤玉が取り出される回数の期待値.ただし,取り出した玉は元に戻さない場合(=非復元抽出の場合)と取り出した玉を元に戻す場合(=復元抽出の場合) (3) 取り出した玉は元に戻さない(=非復元抽出)ものとして,赤玉が出るまで1個ずつ取すときの取り出す回数の期待値と白玉が出るまで1個ずつ取り出すときの取り出す回数の期待値
◆ポイント◆ ⇒「期待値」ときたら「確率分布表」を作る!
(解答)(1) [赤玉の個数] 5個ある玉の中から,2個取り出す方法は,全部で N=5C2=10通り ア) 赤玉0個と白玉2個を取り出す方法は 3C0×2C2=1通り イ) 赤玉1個と白玉1個を取り出す方法は 3C1×2C1=6通り ウ) 赤玉2個と白玉0個を取り出す方法は 3C2×2C0=3通り したがって,赤玉の個数について,確率分布表は次のようになる.
E(X)=0×+1×+2×== [白玉の個数] 5個ある玉の中から,2個取り出す方法は,全部で N=5C2=10通り ア) 赤玉2個と白玉0個を取り出す方法は 3C2×2C0=3通り イ) 赤玉1個と白玉1個を取り出す方法は 3C1×2C1=6通り ウ) 赤玉0個と白玉2個を取り出す方法は 3C0×2C2=1通り したがって,白玉の個数について,確率分布表は次のようになる.
E(Y)=0×+1×+2×== 以上により,赤玉の個数の期待値,白玉の個数の期待値は各々とで,それらの和は2,比は3:2になる.
(参考)
(2)通俗的な感覚(答案に書いても○してもらえない理由付け)だけで言えば,2個のうちで赤玉が含まれる期待値(平均値)が,なら,残りは白玉だから,白玉の期待値(平均値)は2−=となりそうに思える. 実際,後に確率変数の変換の項目で,2つの確率変数X ,YについてE(X+Y)=E(X)+E(Y)が成り立つことが示されるので,X+Y=2 → E(X+Y)=2のとき,E(X)+E(Y)=2という予想が正しいことがわかる. さらにまた,通俗的な感覚だけで言えば,赤玉が3個と白玉が2個あるのだから,赤玉の個数の期待値と白玉の個数の期待値は,:=3:2になっているのではないかと予想できる. 実際,赤玉が3個と白玉が2個あるときに,3個同時に取り出す場合でも,赤玉の個数の期待値と白玉の個数の期待値は,:=3:2が成り立っている.(ただし,この場合は,+=3) ≪非復元抽出の場合≫ [赤玉の個数] 5個ある玉の中から,1個ずつ2回取り出す方法は,全部で N=5×4=20通り ア) 赤玉0個 ⇔ 白−白と出る出方は 2×1=2通り イ) 赤玉1個 ⇔ 赤−白または白−赤と出る出方は 3×2+2×3=12通り(排反事象の加法定理) ウ) 赤玉2個 ⇔ 赤−赤と出る出方は 3×2=6通り したがって,赤玉の個数について,確率分布表は次のようになる.
E(X)=0×+1×+2×==
(参考)
通俗的な感覚(答案に書いても○してもらえない理由付け)だけで言えば,2個同時に取り出すときと,1個ずつ2回取り出すときの,赤玉の個数,白玉の個数の期待値は,結果が一致しているから,いつでも同じになるのではないか,と予想できる. 実際,2個同時に取り出すときは,(組合せ)÷(組合せ)となるのに対して,非復元で1個ずつ取り出すときは(順列)÷(順列)となって,分母・分子とも2!倍になるだけだから,結果は一致する. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
→続き ≪復元抽出の場合≫ [赤玉の個数] 5個ある玉の中から,1個ずつ2回取り出すときに,取り出した玉を元に戻すのだから,その方法は全部で N=5×5=25通り ア) 赤玉0個 ⇔ 白−白と出る出方は 2×2=4通り イ) 赤玉1個 ⇔ 赤−白または白−赤と出る出方は 3×2+2×3=12通り(排反事象の加法定理) ウ) 赤玉2個 ⇔ 赤−赤と出る出方は 3×3=9通り したがって,赤玉の個数について,確率分布表は次のようになる.
E(X)=0×+1×+2×== 以上により,赤玉が取り出されるまでの回数の期待値はいずれもになり,等しい.
(参考)
(3)非復元抽出の場合と復元抽出の場合とで結果が一致する. その理由を,通俗的(答案に書いても○してもらえない理由付け)に考えてみると,復元抽出の場合は,玉の数は毎回3:2であるのに対して,非復元抽出の場合は玉の数が減っていくことを考慮に入れる必要がある. すなわち,非復元抽出の場合,1回目に赤玉が出る確率は0.6,白玉が出る確率は0.4だから,2回目を取るときには,全部で4個のうちに赤玉が2.4個,白玉が1.6個,3:2の割合で含まれることになり,赤の「濃さ」は変わらない.(元が濃いと出やすいから,取った玉を戻さない場合でも濃さは変わらない). そのような訳で,復元抽出の場合と非復元抽出の場合とで結果が一致すると考えられる. [赤玉が出るまでの回数] ア) 1回で赤玉が出る確率は イ) 1回目に白玉が出て,2回目に赤玉が出る確率は ×= ウ) 1回目,2回目とも白玉が出て,3回目に赤玉が出る確率は ×= したがって,赤玉が出るまでの回数について,確率分布表は次のようになる.
E(X)=1×+2×+3×= [白玉が出るまでの回数] ア) 1回で白玉が出る確率は イ) 1回目に赤玉が出て,2回目に白玉が出る確率は ×= ウ) 1回目,2回目とも赤玉が出て,3回目に白玉が出る確率は ××= エ) 1回目,2回目,3回目とも赤玉が出て,4回目に白玉が出る確率は ××= したがって,白玉が出るまでの回数について,確率分布表は次のようになる.
E(X)=1×+2×+3×+4×=2 したがって,赤玉が出るまでの回数の期待値は回,白玉が出るまでの回数の期待値は2回
(参考)
通俗的な感覚だけで言えば,赤玉の方が多く入っているので,赤玉が出るまでの回数の方が少なくなるはずであるが,玉が3:2の割合で入っているときに,出るまでの回数が3:4となる関係(他の比率でも通用する関係)を示すのは簡単ではない. |
 【問題2】
【問題2】 【問題3】
【問題3】

 【問題7】
【問題7】