正方行列のｎ乗

■一般の行列のｎ乗
　左から掛ける行列の列数と右から掛ける行列の行数が等しいときだけ行列の積が定義されるので，行数と列数が異なる行列については２乗は定義されません．したがって，３乗以上の累乗も定義されません．

【２乗が定義できない例】

$A=\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix}$ のとき $A^2=\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix} \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6\end{pmatrix}$ を計算しようとしても，例えば (1,1)成分を求めるときに

$\begin{pmatrix} 1 & 2 & 3 \end{pmatrix} \begin{pmatrix} 1 \\ 4 \end{pmatrix}$ となって，３の相手がいない．他の成分についても同様

■正方行列のｎ乗

正方行列については，次のように順次２乗，３乗，４乗・・・を定義することができます。

Ａ²＝Ａ・Ａ

Ａ^ｎ＝Ａ^ｎ-1・Ａ　（＝Ａ・Ａ^ｎ-1）

ｎが大きくなると行列のｎ乗の成分を求める計算は，特別な例外を除けば，膨大な計算量となります。

■Ａ^ｎの計算機

入力可能な文字は，「半角数字(0～9)」「小数点(. )」及び「符号のマイナス( - )」です。（a,b,x,nなどの文字式は使えません）
上の表のＡの成分を入力し、下のボタンをクリックすれば，Ａの累乗が計算できます。

■研究
上の表を利用して２，３の実験を行うことにより，次の性質が成り立つことを確かめることができます。

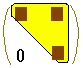
右図のように，行番号ｉ≠列番号ｊ　となる成分が0となる行列は対角行列と呼ばれます。対角行列のｎ乗は，対角行列になります。 $\begin{pmatrix} \lambda & 0 \\ 0 & \mu \end{pmatrix}^n = \begin{pmatrix} \lambda ^n & 0 \\ 0 & \mu ^n \end{pmatrix}$	ｎ
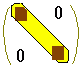
右図のように，行番号ｉ＞列番号ｊ　となる成分が0となる行列は上三角行列と呼ばれます。上三角行列のｎ乗は，上三角行列になる。 $\begin{pmatrix} a & b \\ 0 & c \end{pmatrix} \begin{pmatrix} x & y \\ 0 & z \end{pmatrix}$ において(2,1)成分は $0\times x+ c\times 0=0$ になります	ｎ
右図のように，行番号ｉ＜列番号ｊ　となる成分が0となる行列は下三角行列と呼ばれます。下三角行列のｎ乗は，下三角行列になります。 $\begin{pmatrix} a & 0 \\ b & c \end{pmatrix} \begin{pmatrix} x & 0 \\ y & z \end{pmatrix}$ において(1,2)成分は $a \times 0 + 0 \times z=0$ になります	ｎ

【問題】　次の行列を計算して，正しいものを下の選択肢から選んでください． (1) $\begin{pmatrix} 1 \\ 3 \end{pmatrix} ^2$ 解説 $\begin{pmatrix} 2 \\ 6 \end{pmatrix}$ $\begin{pmatrix} 1 \\ 9 \end{pmatrix}$ $\begin{pmatrix} 1 & 3 \\ 1 & 3 \end{pmatrix}$ 定義されない $\begin{pmatrix} 1 \\ 3 \end{pmatrix}$ は２行１列形の行列で，行数と列数が異なるので，２乗は定義されません．	(2) $\begin{pmatrix} 1 & 0 & 2 \\ 0 & -1 & 0 \end{pmatrix} ^2$ 解説 $\begin{pmatrix} 1 & 0 & 4 \\ 0 & 1 & 0\end{pmatrix}$ $\begin{pmatrix} 5 & 0 \\ 0 & 1\end{pmatrix}$ $\begin{pmatrix} 1 & 0 & 2 \\ 0 & 1 & 0 \\ 2 & 0 & 4\end{pmatrix}$ 定義されない $\begin{pmatrix} 1 & 0 & 2 \\ 0 & -1 & 0 \end{pmatrix}$ は２行３列形の行列で，行数と列数が異なるので，２乗は定義されません．
(3) $\begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix}^4$ 解説 $\begin{pmatrix} 4 & 0 \\ 0 & 9 \end{pmatrix}$ $\begin{pmatrix} 8 & 0 \\ 0 & 12 \end{pmatrix}$ $\begin{pmatrix} 16 & 0 \\ 0 & 81 \end{pmatrix}$ 定義されない対角行列のｎ乗は，各成分をｎ乗を成分すれば求められます $\begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix}^2 =\begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix}\begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix}=\begin{pmatrix} 4 & 0 \\ 0 & 9 \end{pmatrix}$ $\begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix}^3 =\begin{pmatrix} 4 & 0 \\ 0 & 9 \end{pmatrix}\begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix}=\begin{pmatrix} 8 & 0 \\ 0 & 27 \end{pmatrix}$ $\begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix}^4 =\begin{pmatrix} 8 & 0 \\ 0 & 27 \end{pmatrix}\begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix}=\begin{pmatrix} 16 & 0 \\ 0 & 81 \end{pmatrix}$	(4) $\begin{pmatrix} 1 & a \\ 0 & 1 \end{pmatrix}^3$ 解説 $\begin{pmatrix} 1 & 3a \\ 0 & 1 \end{pmatrix}$ $\begin{pmatrix} 1 & a^3 \\ 0 & 1 \end{pmatrix}$ $\begin{pmatrix} 1 & 0 \\ 3a & 1 \end{pmatrix}$ 定義されない $\begin{pmatrix} 1 & a \\ 0 & 1\end{pmatrix}^2 =\begin{pmatrix} 1 & a \\ 0 & 1 \end{pmatrix}\begin{pmatrix} 1 & a \\ 0 & 1 \end{pmatrix}=\begin{pmatrix} 1 & 2a \\ 0 & 1\end{pmatrix}$ $\begin{pmatrix} 1 & a \\ 0 & 1 \end{pmatrix}^3 =\begin{pmatrix} 1 & 2a \\ 0 & 1 \end{pmatrix}\begin{pmatrix} 1 & a \\ 0 & 1 \end{pmatrix}=\begin{pmatrix} 1 & 3a \\ 0 & 1 \end{pmatrix}$ になります
(5) $\begin{pmatrix} 2 & 0 \\ 3 & 0 \end{pmatrix}^2$ 解説 $\begin{pmatrix} 4 & 0 \\ 9 & 0 \end{pmatrix}$ $\begin{pmatrix} 0 & 4 \\ 0 & 9\end{pmatrix}$ $\begin{pmatrix} 4 & 0 \\ 6 & 0 \end{pmatrix}$ 定義されない $\begin{pmatrix} a & 0 \\ b & 0 \end{pmatrix}^2 =\begin{pmatrix} a & 0 \\ b & 0 \end{pmatrix}\begin{pmatrix} a & 0 \\ b & 0 \end{pmatrix}=\begin{pmatrix} a^2 & 0 \\ ab & 0 \end{pmatrix}$ のように各成分を $a$ $ \displaystyle a $倍したものになります $\begin{pmatrix} 4 & 0 \\ 6 & 0 \end{pmatrix}$	(6) $\begin{pmatrix} 0 & 0 \\ 3 & 4 \end{pmatrix}^2$ 解説 $\begin{pmatrix} 0 & 0 \\ 12 & 16 \end{pmatrix}$ $\begin{pmatrix} 0 & 0 \\ 9 & 16 \end{pmatrix}$ $\begin{pmatrix} 0 & 12 \\ 0 & 16 \end{pmatrix}$ 定義されない $\begin{pmatrix} 0 & 0 \\ x & y \end{pmatrix}^2 =\begin{pmatrix} 0 & 0 \\ x & y \end{pmatrix}\begin{pmatrix} 0 & 0 \\ x & y \end{pmatrix}=\begin{pmatrix} 0 & 0 \\ xy & y^2 \end{pmatrix}$ のように各成分を $y$ $ \displaystyle y $倍したものになります $\begin{pmatrix} 0 & 0 \\ 12 & 16 \end{pmatrix}$

..高卒～大学数学のメニューに戻る　 ●==メニューに戻る