|
【1次変換とは】 ■集合から集合への対応 f:A→B のうち,f:A→A のように,同一集合への対応を変換といいます。 ■x,y平面上の点からx,y平面上の点への対応 のうち, x’=ax+by y’=cx+dy ■1次変換は,行列を用いて 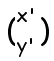 = =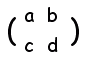 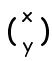 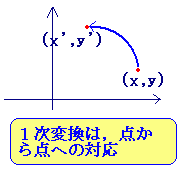 |
|
【1次変換とは】 ■集合から集合への対応 f:A→B のうち,f:A→A のように,同一集合への対応を変換といいます。 ■x,y平面上の点からx,y平面上の点への対応 のうち, x’=ax+by y’=cx+dy ■1次変換は,行列を用いて 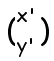 = =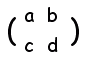 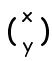  |
|
【1次変換の例】 ■1 x軸に関する対称移動 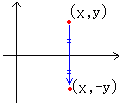
y’=−y y’=0・x+(-1)・y
x軸に関する対称移動を表す1次変換の行列は
■2
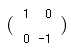 y軸に関する対称移動 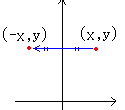
y’=y y’=0・x+1・y
y軸に関する対称移動を表す1次変換の行列は
■3
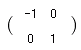 原点に関する対称移動 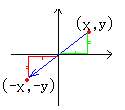
y’=−y y’=0・x+(-1)・y
原点に関する対称移動を表す1次変換の行列は
■4
 y=xの直線に関する対称移動 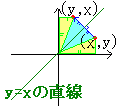
(授業では,この部分の誤解が特に多いので注意 「y=x」という言葉に惑わされることなく,図で考えることが大切) y’=x y’=1・x+0・y
y=xの直線に関する対称移動を表す1次変換の行列は
■5
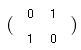 y=−xの直線に関する対称移動 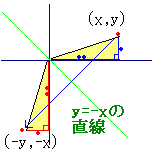
y’=−x y’=(-1)・x+0・y
y=-xの直線に関する対称移動を表す1次変換の行列は
■6
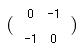 恒等変換すなわち各点を自分自身に対応させる変換は, y’=y y’=0・x+1・y
恒等変換を表す1次変換の行列は
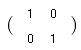 |
|
■(簡単)確認テスト 次の行列が表す1次変換を右から選びなさ い。(初めに問題を選び,次に選択肢を選びなさい。) 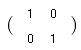
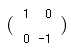 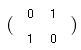
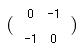 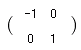
 
 
 

 |
|
[注]直前にPC版から入られた場合は,自動転送でスマホ版に来ていますので,ブラウザの[戻るキー]では戻れません(堂々巡りになる).下記のリンクを使ってメニューに戻ってください.
|
|
■[個別の頁からの質問に対する回答][1次変換について/17.4.9]
とても良い!
■[個別の頁からの質問に対する回答][1次変換について/17.2.22]
=>[作者]:連絡ありがとう.この教材は,実際には体験・入門レベルの内容ですが,この教材でよい評価が得られる理由として,教育課程の改訂とか科目選択の都合で,そもそも習っていない方が読んでいる場合があるのかなと真剣に考えています. 東工大受験3日前に良い勉強できました。回転座標の問題や明らかに行列式をモチーフにした問題が出たら是非複素平面といった回りくどい方法を取らずにバッチリ一次変換を使って行きたいと思います
■[個別の頁からの質問に対する回答][1次変換について/17.2.21]
=>[作者]:連絡ありがとう. とてもわかりやすいです。参考になりました。
=>[作者]:連絡ありがとう. |