|
■2点とその像→変換式 ■2点とその像が与えられた場合,元の変換式を求め ることができます。 例 (−2,1)が(−5, 4)に移されるとき, 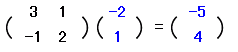 ・・(1) ・・(1) |
※ 逆行列がないときは,求められません。
|
|
■2点とその像→変換式 ■2点とその像が与えられた場合,元の変換式を求め ることができます。 例 (−2,1)が(−5, 4)に移されるとき, 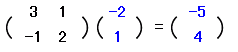 ・・(1) ・・(1) |
※ 逆行列がないときは,求められません。
|
| ■
例題1
点(2,−1)を点(1,0)に,点(1,2)を点(8,5)に移す1次変換の行列を求めなさ い。 [答案例] 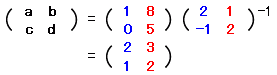 ・・答 ・・答 |
■例題2
点(1,0)を点(3,5)に,点(0,1)を点(4,-3)に移す1次変換の行列を求めなさ い。 [答案例] |
| [問題]--計算用紙が必要です。
正答:  ,誤答: ,誤答:
1 点(1,1)を点(2,4)に,点(2,3)を点(2,5)に移す1次変換の行列を求めなさ い。 |
 |
|
|
解説 |
||
|
2
点(1,0)を点(3,2)に,点(0,1)を点(1,−5)に移す1次変換の行列を求めなさ い。 |
 |
|
|
解説 \( \displaystyle \begin{pmatrix} a & b \\ c & d \end{pmatrix}\Big(\begin{matrix} 1 \\ 0 \end{matrix}\hspace{10px}\begin{matrix} 0 \\ 1 \end{matrix}\Big) \) \( \displaystyle =\Big(\begin{matrix} 3 \\ 2 \end{matrix}\hspace{10px}\begin{matrix} 1 \\ -5 \end{matrix}\Big) \) \( \displaystyle \begin{pmatrix} a & b \\ c & d \end{pmatrix}=\begin{pmatrix} 3 & 1 \\ 2 & -5 \end{pmatrix} \) |
||
| 3
点(1,−1)を点(1,1)に,点(0,1)を点(2,4)に移す1次変換の行列を求めなさ い。 |
 |
|
|
解説 \(\displaystyle \begin{pmatrix} a & b \\ c & d \end{pmatrix}\begin{pmatrix} 1 \\ -1 \end{pmatrix}=\begin{pmatrix} 1 \\ 1 \end{pmatrix}\) \(\displaystyle \begin{pmatrix} a & b \\ c & d \end{pmatrix}\begin{pmatrix} 0 \\ 1 \end{pmatrix}=\begin{pmatrix} 2 \\ 4 \end{pmatrix}\) \(\displaystyle \begin{pmatrix} a & b \\ c & d \end{pmatrix}\Big(\begin{matrix} 1 \\ -1 \end{matrix}\hspace{10px}\begin{matrix} 0 \\ 1 \end{matrix}\Big)=\Big(\begin{matrix} 1 \\ 1 \end{matrix}\hspace{10px}\begin{matrix} 2 \\ 4 \end{matrix}\Big) \) \(\displaystyle \begin{pmatrix} a & b \\ c & d \end{pmatrix}=\begin{pmatrix} 1 & 2 \\ 1 & 4 \end{pmatrix}\begin{pmatrix} 1 & 0 \\ -1 & 1 \end{pmatrix}^{-1} \) \(\displaystyle =\begin{pmatrix} 1 & 2 \\ 1 & 4 \end{pmatrix}\begin{pmatrix} 1 & 0 \\ 1 & 1 \end{pmatrix}=\begin{pmatrix} 3 & 2 \\ 5 & 4 \end{pmatrix} \) |
||