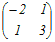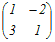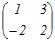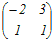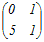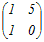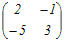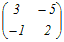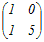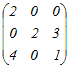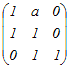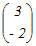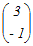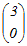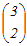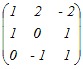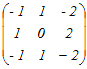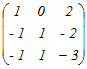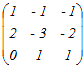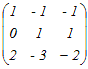|
■逆行列 → 印刷用PDF版は別頁
【逆行列とは】
n次正方行列Aに対して AB=BA=En が成り立つとき,n次正方行列BをAの逆行列といい,A−1で表す.ここに,Enはn次の単位行列とする.
【例】
※n次正方行列Aの逆行列A−1が存在するとき(1) 2次の正方行列について 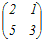 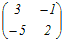 = =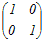 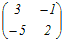 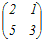 = =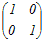 だから 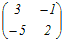 は は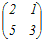 の逆行列 の逆行列また, 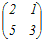 は は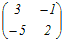 の逆行列 の逆行列(2) 3次の正方行列について 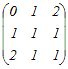 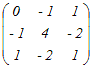 = =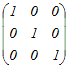 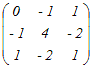 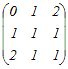 = =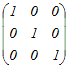 だから 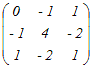 は は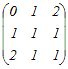 の逆行列 の逆行列また, 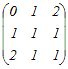 は は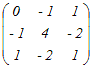 の逆行列 の逆行列AA−1=A−1A=En が成り立つ. ※正方行列でないものについては逆行列は考えない.
【逆行列の求め方】
○2次の正方行列について,高校では(教育課程により,また科目選択により,習わないことがある)次のように覚える.
(ア) |A|=ad−bc≠0のとき,逆行列が存在し
○3次以上の正方行列については,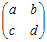 の逆行列は の逆行列は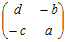 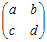 の対角成分は入れ替えて,対角でない成分は符号だけ変えたもの の対角成分は入れ替えて,対角でない成分は符号だけ変えたもの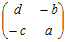 を考えると, を考えると,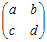 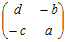 = =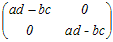 となるから,全体をad−bcで割ると単位行列になる. A= 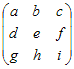 の逆行列を求めるには,その右側に単位行列を付けた次のような行列を考えて の逆行列を求めるには,その右側に単位行列を付けた次のような行列を考えて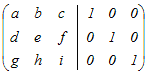 |
○この頁に登場する【問題】は,公益社団法人日本技術士会のホームページに掲載されている「技術士第一次試験過去問題 共通科目A 数学」の引用です.(=公表された著作物の引用)
○【解説】は個人の試案ですが,Web教材化にあたって「問題の転記ミス」「考え方の間違い」「プログラムの作動ミス」などが含まれる場合があり得ます. 問題や解説についての質問等は,原著作者を煩わせることなく,当Web教材の作成者(<浅尾>)に対して行ってください.
(逆行列の求め方)
【例】 (1) (高校数学で習う方法で)A= 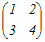 の逆行列を求めるには,まず対角成分は入れ替えて,対角でない成分は符号だけ変えて の逆行列を求めるには,まず対角成分は入れ替えて,対角でない成分は符号だけ変えて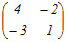 を考える.次に,これを行列式|A|=4−6=−2で割って
A−1= を考える.次に,これを行列式|A|=4−6=−2で割って
A−1=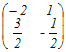 とする.
行基本変形で求めるには とする.
行基本変形で求めるには右側に単位行列を付けた次のような行列を考える 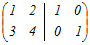 1行目は左端が1になっている.2行目から1行目の3倍を引く 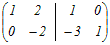 2行目の0でない左端を1にするために,2行目を−2で割る 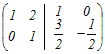 1行目から2行目の2倍を引いて,左側の行列を単位行列にする 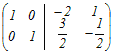 よって, 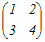 −1= −1=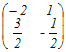 (2)
(2)行基本変形によって 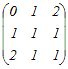 の逆行列を求めるには,はじめに右側に単位行列を付けた次のような行列を考える の逆行列を求めるには,はじめに右側に単位行列を付けた次のような行列を考える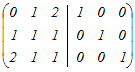 1行目と2行目を入れ替える 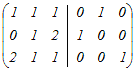 3行目から1行目の2倍を引く 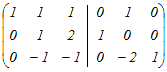 1行目から2行目を引く,3行目に2行目を足す 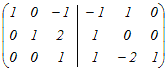 1行目に3行目を足す,2行目から3行目の2倍を引く 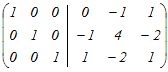 よって, 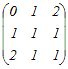 −1= −1=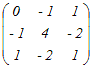
|
|
A
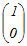 = =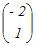 A 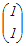 = =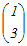 のとき,これらをまとめて A 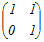 = =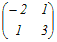 と表せるから 両辺に右から 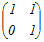 −1を掛けると −1を掛けるとA= 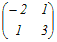 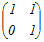 −1= −1=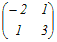 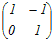 = =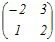 → 3
→ 3≪別解≫
A=
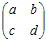 とおくと とおくとA 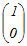 = =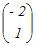 よりa=−2, c=1 よりa=−2, c=1A 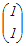 = =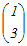 よりa+b=1, c+d=3 よりa+b=1, c+d=3だから a=−2, b=3, c=1, d=2 A= 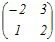
|
AB+2B=Eより
(A+2E)B=E 両辺に左から(A+2E)−1を掛けると B=(A+2E)−1 A+2E= 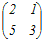 だから だからB=(A+2E)−1= 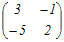 → 3
→ 3 |
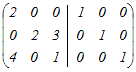 から行基本変形を行って,逆行列を求める から行基本変形を行って,逆行列を求める1行目を2で割る 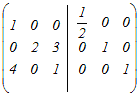 3行目から1行目の4倍を引く 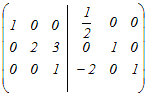 2行目から3行目の3倍を引く 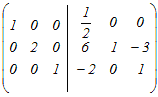 2行目を2で割る 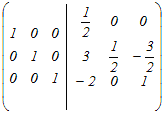 逆行列A−1の(1, 1)成分は → 1 |
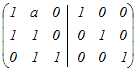 から行基本変形を行う から行基本変形を行う2行目から1行目を引く 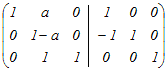 2行2列の成分1−aが0の場合は,2行目のすべての成分が0となるため,行列式が0となり,逆行列が存在しない.これは題意に合わないからa≠0といえる.そこで2行目を1−aで割る. 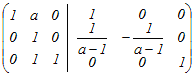 1行目から2行目のa倍を引く.3行目から2行目を引く 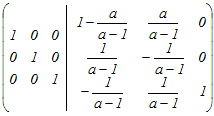 できた逆行列の(1, 1)成分が−1であるから 1−=−1 a−1−a=−(a−1) a=2 → 5 |
|
≪逆行列を利用する方法≫
A 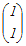 = =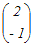 A 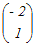 = =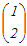 だから A 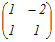 = =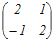 A= 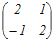 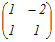 −1= −1=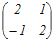 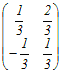 = 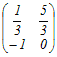 したがって A 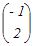 = =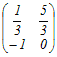 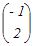 = =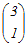 → 4 → 4≪行列の積の線形性を利用する方法≫
行列A,列ベクトル, , , について
A=,A= ならば A(+)=+ が成り立つ 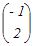 = =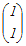 + +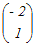 だから A 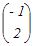 =A =A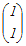 +A +A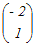 = =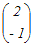 + +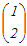 = =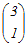 |
≪必要なところだけ計算する≫
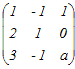 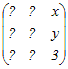 = =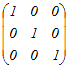 となるから,積の3列目だけ比較すると x−y+3=0…(1) 2x+y=0…(2) 3x−y+3a=1…(3) (1)(2)よりx=−1, y=2 これを(3)に代入 a=2 → 5 ≪別解:行基本変形により逆行列を求める≫ 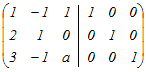 から変形し始める から変形し始める2行目から1行目の2倍を引く.3行目から1行目の3倍を引く 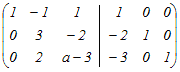 2行目を3で割る 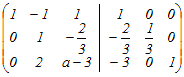 1行目に2行目を足す.3行目から2行目の2倍を引く 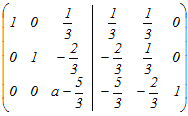 3行目にを掛ける 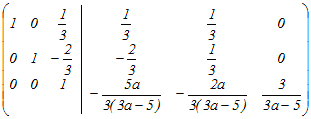 まだ途中であるが,以下の変形は逆行列の(3,3)成分に影響しない.逆行列の(3,3)成分が3だから =3 3a−5=1 a=2 |
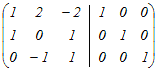 から行基本変形によって求める から行基本変形によって求める2行目から1行目を引く 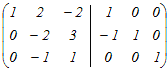 (分数を避けるために)2行目と3行目を入れ替える 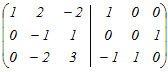 2行目の符号を変える 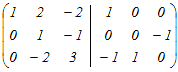 1行目から2行目の2倍を引く.3行目に2行目の2倍を足す 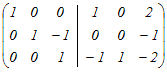 2行目に3行目を足す 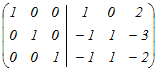 よって,逆行列は 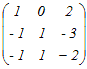 → 3
→ 3
|
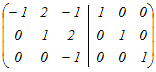 から行基本変形で求める から行基本変形で求める1行目の符号を変える 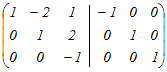 1行目に2行目の2倍を足す 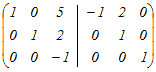 3行目の符号を変える 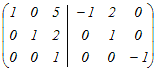 1行目から3行目の5倍を引く.2行目から3行目の2倍を引く 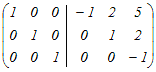 よって、逆行列は 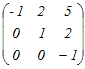 → 1
→ 1
|