|
(1.1) 正の数
1) ガンマ関数について,次の関係が成り立つ. 2) 3) 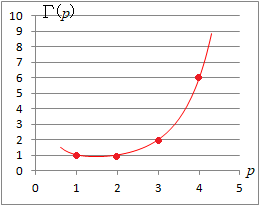 |
(証明) 1) 次の部分積分を行う 2) 1)の結果を使うと ここで だから 3) 後出(1.3) 1)により示される. |
|
(1.1) 正の数
1) ガンマ関数について,次の関係が成り立つ. 2) 3)  |
(証明) 1) 次の部分積分を行う 2) 1)の結果を使うと ここで だから 3) 後出(1.3) 1)により示される. |
|
(1.2)
1) 2) 置換積分により,次の式を示せる. 3) ベータ関数はガンマ関数と次の関係にある. 4) ベータ関数\(B(m, n)\)は\(m, n\gt 0\)で定義されるが,特に\(m, n\)が正(または0)の整数のとき,次のように階乗で表せる. |
(証明) 1) において,次の置換積分を行う 2) に対して次の置換積分を行う |
|
3) のような2つの積分の積を と結び付けるには,1つの重積分として直交座標から極座標へ変換する方法が考えられる.その場合, とするために,2乗の形をした式が使いやすい. において, 同様にして これらの積を求めると |
ここで,
ヤコビアンは だから 4) (1.1) 2)により, だから |
|
(1.3) 誤差関数(error function→erf)
1) ガウスの積分公式 2) 3) 4) 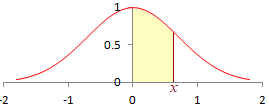 (1.3)の誤差関数は,初等的に(多項式,分数関数,無理関数,指数関数,対数関数,三角関数,およびそれらの有限回の組合せや合成)では書けない.
(1.3)の誤差関数は,初等的に(多項式,分数関数,無理関数,指数関数,対数関数,三角関数,およびそれらの有限回の組合せや合成)では書けない.右図のような正規分布(ただし定数倍の調整あり)で0〜xまでの面積を表す. 1) 誤差関数で積分区間が0〜無限の定積分は,ガウスの積分公式と呼ばれ,値を求めることができる. 重積分を利用する次の方法がよく見られる. とおくと |
ここで,
ヤコビアンは だから |
|
2)← 1)において, したがって,1)の結果から 3)← 1)において, |
1)の結果から 偶関数だから 結局 4)← 1)において, 1)の結果から したがって |
|
Γ関数,B関数について,次の値を求めてください.
【問題1-1】
(解答)(1.1) 2)により, だから
【問題1-2】
(解答)(1.1) 1)により, さらに,(1.1) 3)により, だから, |
【問題1-3】
(解答)(1.2) 4)により,
【問題1-4】
(解答)(1.2) 3)により, |
|
【問題1-5】
(解答)ガンマ関数の定義 において, だから |
【問題1-6】
(解答)をΓ関数を用いて表してください. ただし, ベータ関数の定義およびガンマ関数との関係式 において の変換により置換積分を行うと だから |
|
【問題1-7】
(解答)をベータ関数を使って表してください. ベータ関数の定義式 において の変換により置換積分を行うと ここで を代入すると
【問題1-8】
(解答)をベータ関数を使って表してください. 前問とほぼ同様の途中経過でできます. |
【問題1-9】
(解答)をベータ関数を使って表してください.ただし, (1.2) 2)の式 において を代入すると だから
【問題1-10】
(解答)に対して次の部分積分で変換する. |