|
■微分方程式...変数変換による解き方 ○ 1階の常微分方程式について,何らかの変数変換を行うことによって解きやすい形に変えることは,この頁以前にも登場しています. ◆◆◆ 復習 ◆◆◆
(I)同次形の微分方程式
[ポイント]=f()の形に書けるものは,z=とおけば zがxに関して変数分離形になります. z= ⇔ y=zxとおけば =x+z だから x+z=f(z) となって x=f(z)−z 右辺がzだけの式になり = 変数分離形になります
(II)ベルヌーイ形の微分方程式
[ポイント]y'+P(x)y=Q(x)yn (n≠0, 1) の形に書けるものは, y−n y'+P(x)y1−n=Q(x) と変形してz=y1−nとおけば, zがxに関して線形微分方程式になります. z=y1−nとおけば z'=(1−n)y−n y' となって z'+P(x)z=Q(x) は線形微分方程式になります.
(III)リッカチ形の微分方程式
[ポイント]y'+P(x)y2+Q(x)y+R(x)=0 の形に書けるものは,その1つの特別解y1がわかれば,y=y1+zとおくことにより,zがxに関してベルヌーイ形の微分方程式になります. y1'+P(x)y12+Q(x)y1+R(x)=0 だから,y1がR(x)を”持って行ってしまう”ので,残りのzについては z'+S(x)z2+T(x)z=0 となってベルヌーイ形になります. |
(I)の例
x2y'−xy+2y2=0
y'==−2()2 において,z=とおけば
一般解は
z'x+z=z−2z2y= になります. z'x=−2z2 =− =−dx となって変数分離形になります. (II)の例
xy'+y=xy2
y'+=y2
一般解は
y−2 y'+y−1=1=−log|x|+C になります. においてz=y−1とおけば z'=−y−2 y' だから −z'+z=1 z'−z=−1 は線形微分方程式になります.(この結果は同次形と見なしても解けます.) (III)の例
xy'−y+y2=x2
y1=xが1つの特別解になるから,y=x+uとおくと,uは次のベルヌーイ形の微分方程式を満たします.u'+(2−)u=− u−2 u'+(2−)u−1=− においてw=u−1とおけば w'+(−2)w= は線形微分方程式になります.
一般解は,順に
になります. |
|
◆◆◆この頁で扱う内容◆◆◆ …上記以外で,変数変換によって既知の解き方に持ち込めるもの
(IV)y'=f(ax+by+c)
[ポイント]の形に書けるものは,z=ax+by+cとおくことにより,zがxに関して変数分離形の微分方程式になります. z'=a+by' ⇔ y'=だから,
←yが全部取れたらOK
=f(z)z'=bf(z)+a は変数分離形になります.
【例IV.1】
(解答)y'=の一般解を求めてください. z=2x+y−1とおくと z'=2+y' ⇔ y'=z'−2になるから z'−2=
一般解は
z'=y=Ce−2x−5 は変数分離形になります.
【例IV.2】
(解答)y'=の一般解を求めてください.
※この問題のように,右辺の分子と分母のx,yの係数について,a'x+b'y+c' / ax+by+cとしたときに
(解答)a'=ka, b'=kbを満たすとき すなわち分母=0が表す直線と分子=0が表す直線が平行になっているとき(定数項cは同じ比でない) a'x+b'y+c'=k(ax+by+c)+...の形に書くことができます. 4x−2y+3=2(2x−y+1)+1だから z=2x−y+1とおくと (右辺)= また,z'=2−y'だから (左辺)=2−z' したがって方程式は
一般解は
2−z'=(2x−y+1)2+2x=C になります. z'=− となって,変数分離形になります. |
(V)y'=f()だたしa:a'≠b:b'
[ポイント]の形に書けるものは, 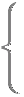 a'x+b'y+c'=0 a'x+b'y+c'=0ax+by+c=0 の連立方程式の解をx=p, y=qとするとき(a:a'≠b:b'だから2直線は交わる)
とする変換により,定数項が消えて
Y'=f()の形になるので
z=とおけば,変数分離形になります.
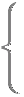 a'p+b'q+c'=0 a'p+b'q+c'=0ap+bq+c=0 が成り立つ場合は 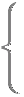 a'(X+p)+b'(Y+q)+c'=a'X+b'Y+(a'p+b'q+c')
a'(X+p)+b'(Y+q)+c'=a'X+b'Y+(a'p+b'q+c')a(X+p)+b(Y+q)+c=aX+bY+(ap+bq+c) において,定数項が消えます.
【例V.1】
(解答)y'=−の一般解を求めてください. 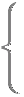 4x+3y−10=0 4x+3y−10=03x−4y+5=0 の解はx=1, y=2だから, y'=−と変形でき, X=x−1, Y=y−2とおくと =− の右辺の分母分子をXで割り,z=とおくと z'X+z=− z'X=− dz=−dX は変数分離形になります.
一般解は
(x+2y−5)(2x−y)=C になります. |
|
z=x−2y+1とおくと
z'=1−2y' ⇔ y'= = =1−z =−dx =−dx log|z−1|=−x+C1 |z−1|=e−x+C1=eC1e−x z−1=±eC1e−x=C2e−x x−2y+1−1=C2e−x x−2y=C2e−x y== →1 |
z=x−yとおくと
z'=1−y' ⇔ y'=1−z' 1−z'= =1− dz=dx は変数分離形 dz=dx これを計算して,最後にx,yに戻す =Ce2y→3 |
|
z=2x+y+3とおくと
z'=2+y' ⇔ y'=z'−2 z'−2=− z'= は変数分離形になる. これを解くと z2=2x+C (2x+y+3)z2−2x=C →2 |
連立方程式6x−5y+21=0 , 5x+4y−7=0の解はx=−1 , y=3
= X=x+1 , Y=y−3とおくと,dX=dx , dY=dy = 右辺の分母分子をXで割って,z=とおくと z'X+z= z'X=− dz=−dX は変数分離形になる. これを解くと (2y−x−7)(y+3x)=C→4 |
|
(VI)=f(xy)
[ポイント]の形に書けるものは,z=xyとおくと変数分離形になります. z=xyのときz'=y+xy' ⇔ y'= =f(z) z'−y=yf(z) z'−=f(z) z'=(f(z)+1) = となって変数分離形になります.
【例VI.1】
(解答)=(x2y2−1)の一般解を求めてください. z=xyとおくとz'=y+xy' ⇔ y'= =(z2−1) z'−y=y(z2−1) z'=y(z2−1+1)=yz2= = は変数分離形になるので,これを解いて,最後にx,yに戻します. y2= になります. |
=()
と変形できるので,z=xyとおくと変数分離形になります. …(途中経過略)… dz=dx になり,これを解くと =Ce− 変数をx,yに戻すと =Ce−→2
=()
と変形できるので,z=xyとおくと変数分離形になります. …(途中経過略)… dz= になり,これを解くと =C 変数をx,yに戻すと y(xy+2)=Cx→3 |